Chapter 6 Guyafor

In this chapter, I repeated the model fit for the whole Guyafor network.

6.1 Data

I used only recruited trees in the censuses with at least 4 measurements of diameter at breast height (DBH, cm). I used only species with at least 4 trees following previous requirements (Tab. 6.1 & Fig. 6.1).

Table 6.1: Metrics on inventory data used to fit the full model including sample size (N), memdian, minimum and maximum values for families, genera, species, individuals, observations, cenusus, recruitment year (year0), last censused year (yearmax), recruitment diameter (dbh0) and last censused diameter (dbhmax).
	N	Median	Minimum	Maximum
families	49
genera	155
species	297
individuals	21 769
observations	267 530
census		12	5	30
year0		1 998	1 986	2 011
yearmax		2 021	1 997	2 021
dbh0		11	5	15
dbhmax		14	6	83

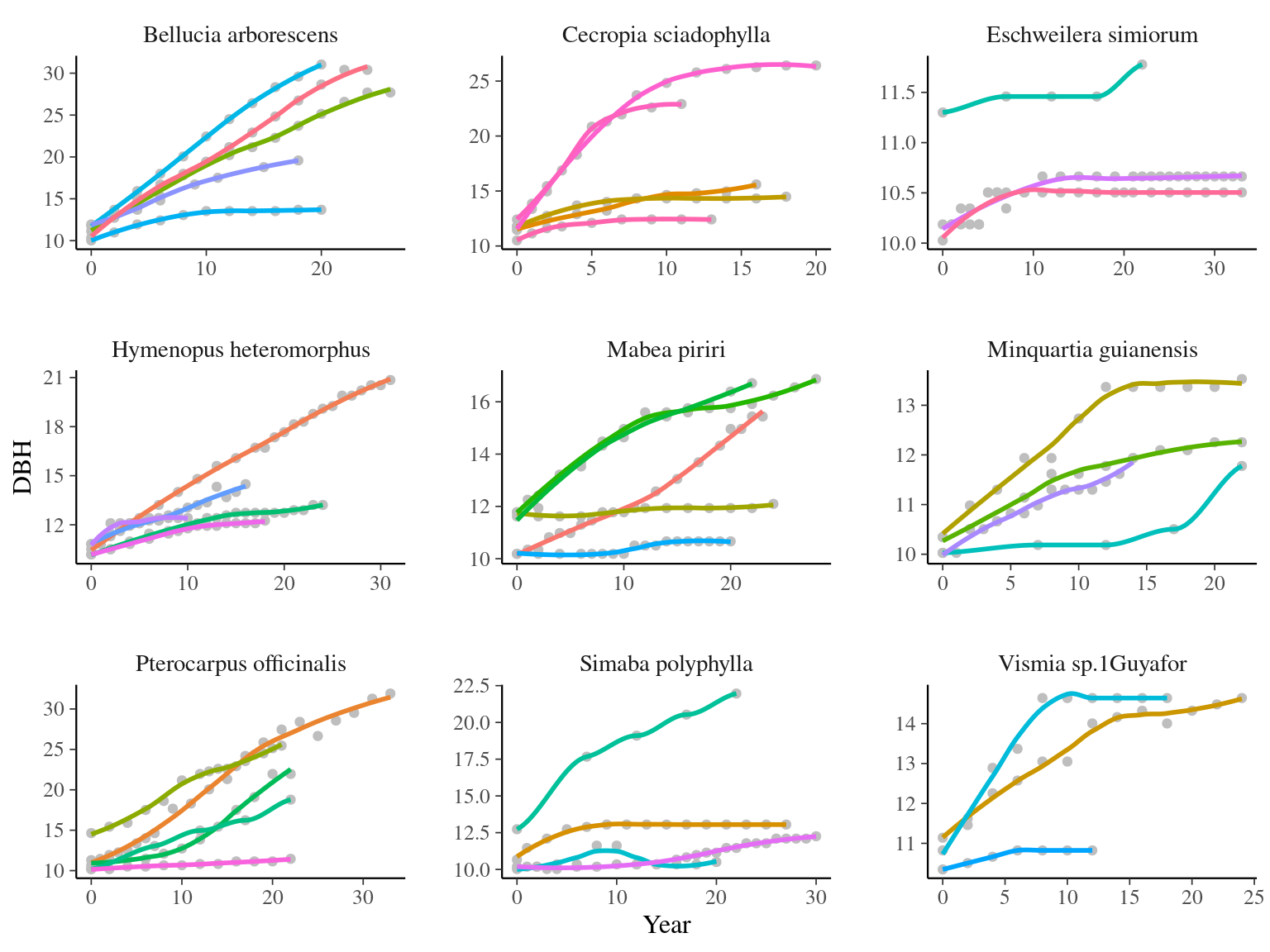
Figure 6.1: Tree diameter trajectories in reduced data. Color represent individuals.

6.2 Model

I used a Gompertz model (Herault2011?), were the diameter of individual \(i\) at year \(t\) is the sum of annual growth from \(t0\) to \(t\):

\[ DBH_{t,i,s} \sim \mathcal N (10 + Gmax_i \times \sum _{y=1|DBH_{t=0}} ^{y=t} exp(-\frac12.[\frac{log(\frac{DBH_{t,i}}{100.Dopt_i})}{Ks_i}]^2)), \sigma) \\| Dopt_i \sim \mathcal N(Dopt_s,\sigma_D), Ks_i \sim \mathcal N(Ks_s,\sigma_K) \]

The annual growth rate for individual \(i\) at year \(y\) with a diameter of \(DBH_{y,i}\) is defined following a Gompertz model (Gompertz 1825) already identified as the best model for growth-trajectories in Paracou (Herault2011?), where \(Gmax_i\) is the fixed maximum growth potential of every individual, \(Dopt_i\) is the optimal diameter at which the individual reaches its maximum growth potential, and \(Ks_i\) is the kurtosis defining the width of the bell-shaped growth-trajectory (see figure 1 in Herault2011?). \(Dopt_i\) and \(Ks_i\) are random effects centered on species parameters \(Dopt_s\) and \(Ks_s\) with associated variances \(\sigma_D\) and \(\sigma_K\).

fit <- read_cmdstan_csv("save/growthguyafor/growth-202210280057-1-361cf6.csv")
draws <- drop(fit$post_warmup_draws) %>% 
  as_data_frame() %>% 
  mutate(iteration = 1:n()) %>% 
  gather(parameter, value, -iteration)
vroom::vroom_write(draws, file = 'save/growthguyafor/chain1.tsv')
rm(fit, draws)
gc()

fit <- read_cmdstan_csv("save/growthguyafor/growth-202210280057-2-361cf6.csv")
draws <- drop(fit$post_warmup_draws) %>% 
  as_data_frame() %>% 
  mutate(iteration = 1:n()) %>% 
  gather(parameter, value, -iteration)
vroom::vroom_write(draws, file = 'save/growthguyafor/chain2.tsv')
rm(fit, draws)
gc()

fit <- read_cmdstan_csv("save/growthguyafor/growth-202210280057-3-361cf6.csv")
draws <- drop(fit$post_warmup_draws) %>% 
  as_data_frame() %>% 
  mutate(iteration = 1:n()) %>% 
  gather(parameter, value, -iteration)
vroom::vroom_write(draws, file = 'save/growthguyafor/chain3.tsv')
rm(fit, draws)
gc()

fit <- read_cmdstan_csv("save/growthguyafor/growth-202210280057-4-361cf6.csv")
draws <- drop(fit$post_warmup_draws) %>% 
  as_data_frame() %>% 
  mutate(iteration = 1:n()) %>% 
  gather(parameter, value, -iteration)
vroom::vroom_write(draws, file = 'save/growthguyafor/chain4.tsv')
rm(fit, draws)
gc()

grep gmax chain1.tsv > gmax1.tsv
grep gmax chain2.tsv > gmax2.tsv
grep gmax chain3.tsv > gmax3.tsv
grep gmax chain4.tsv > gmax4.tsv

bind_rows(
  vroom::vroom('save/growthguyafor/gmax1.tsv', col_names = c("iteration", "parameter", "value")) %>%
  mutate(chain = 1),
  vroom::vroom('save/growthguyafor/gmax2.tsv', col_names = c("iteration", "parameter", "value")) %>%
  mutate(chain = 2),
  vroom::vroom('save/growthguyafor/gmax3.tsv', col_names = c("iteration", "parameter", "value")) %>%
  mutate(chain = 3),
  vroom::vroom('save/growthguyafor/gmax4.tsv', col_names = c("iteration", "parameter", "value")) %>%
  mutate(chain = 4)
) %>% 
  separate(parameter, c("gmax", "ind")) %>% 
  vroom::vroom_write(file = 'save/growthguyafor/gmax.tsv')

library(csv2sql)
gmax <- vroom::vroom(file = 'save/growthguyafor/gmax.tsv')
write_csv(gmax, file = 'save/growthguyafor/gmax.csv')
csv_to_sqlite(csv_name = 'save/growthguyafor/gmax.csv', 
              db_name = 'save/growthguyafor/gmax.sql', 
              table_name = "gmax")
unlink('save/growthguyafor/gmax.csv')

6.3 Fit

Unfortunately, gmax upper limit was set to 5 instead of 10 (overconstrained). But the model with more stringent data had a better behavior with gmax limited to 5.

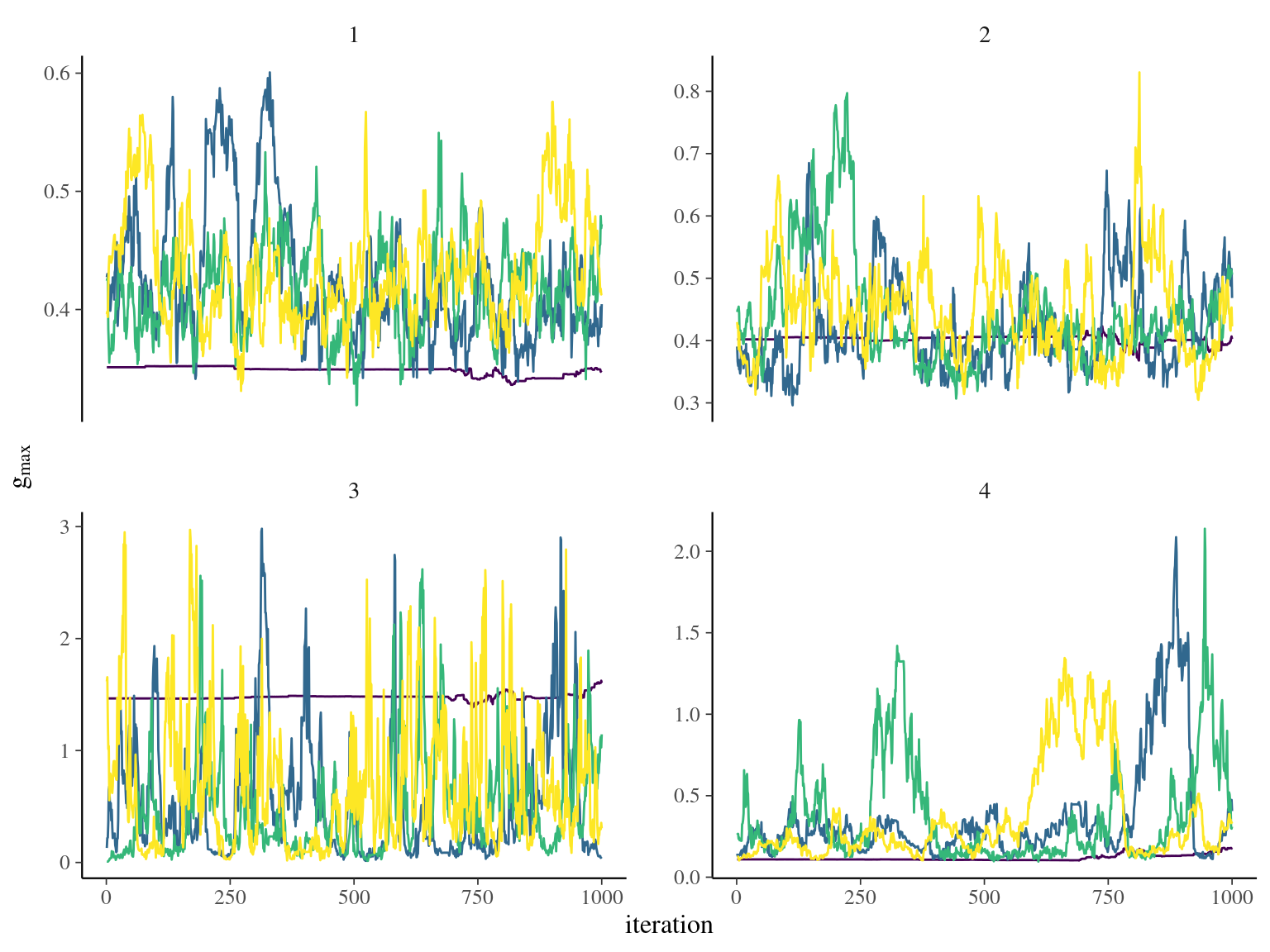
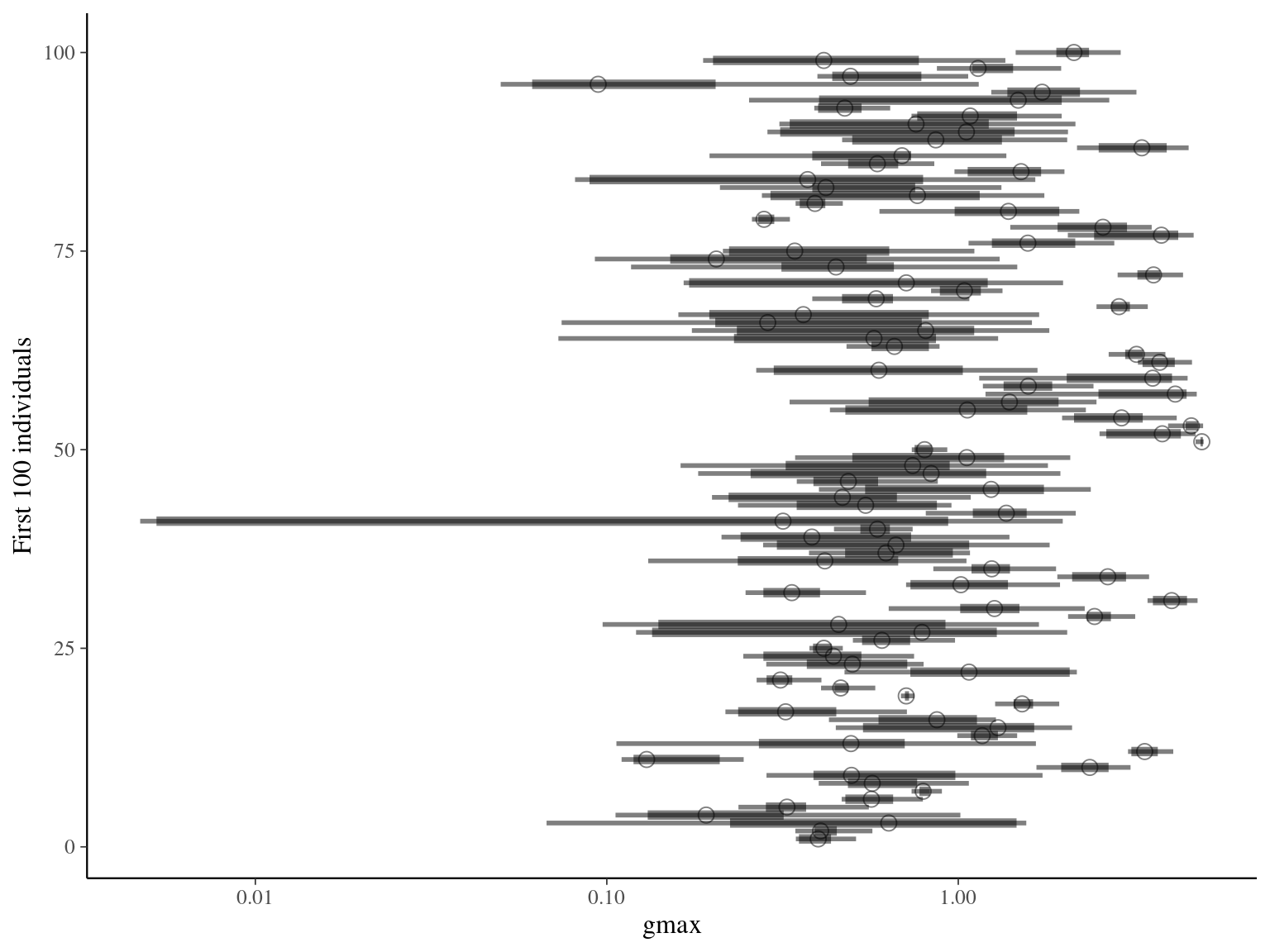
6.4 Evolutionary analyses

Figure 6.2: Distribution of species growth potential (Gmax, cm/yr) in the phylogeny.

6.5 Discussion

Within-chain parallelization available with gompertzsumpar model.
Next steps:
- Stop?
- Use?
- Run again?
  - Cluster?
  - Who?
  - When?
- What for? Data paper?

References

Gompertz, B. (1825). On the nature of the function expressive of the law of humanmortality, and on a newmode of determining the value of life contingencies. Philosophical Transactions of the Royal Society of London, 115, 513–583. Retrieved from https://www.tandfonline.com/doi/full/10.1080/14786445908642737