Chapter 2 Species integration

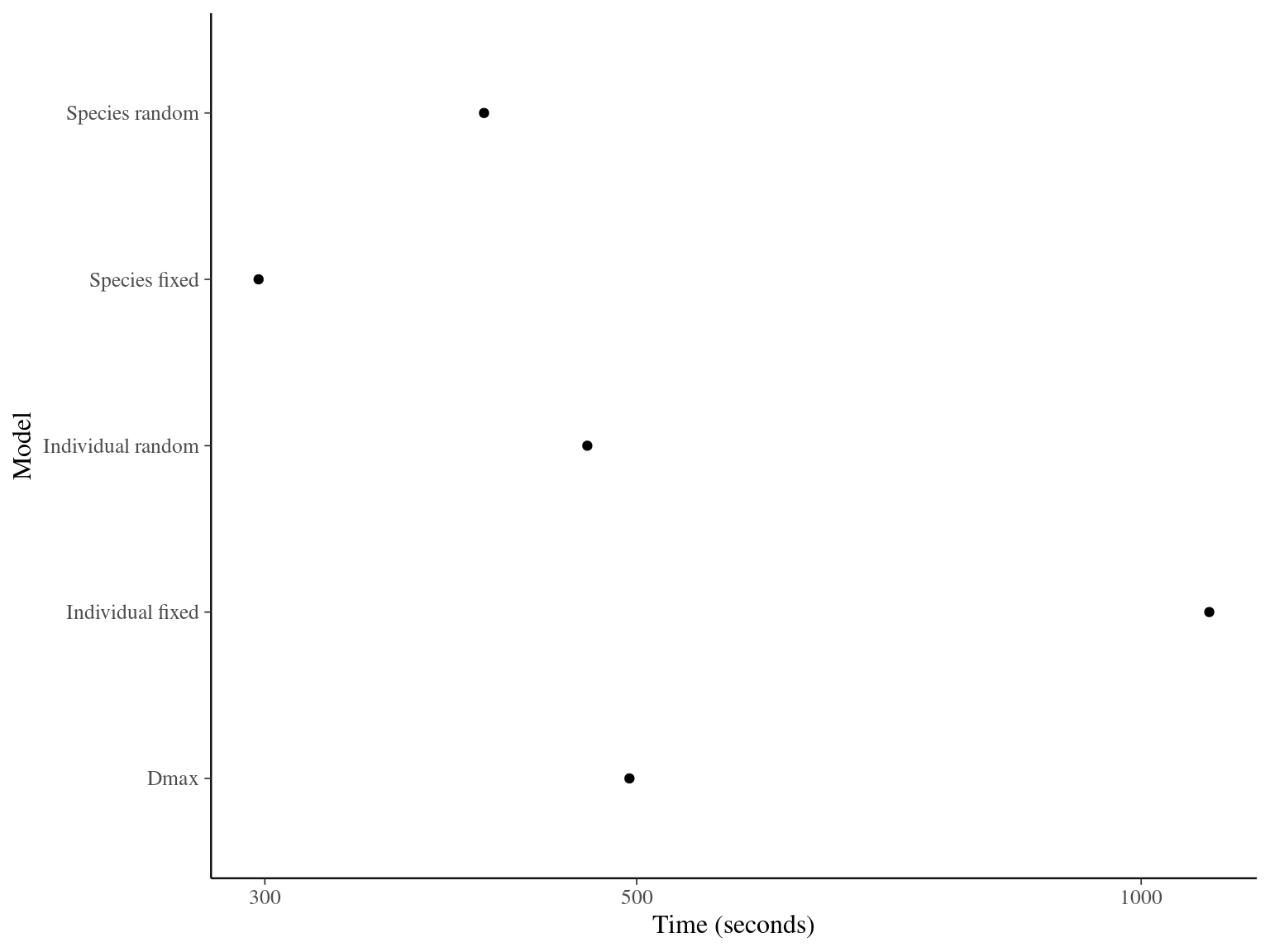
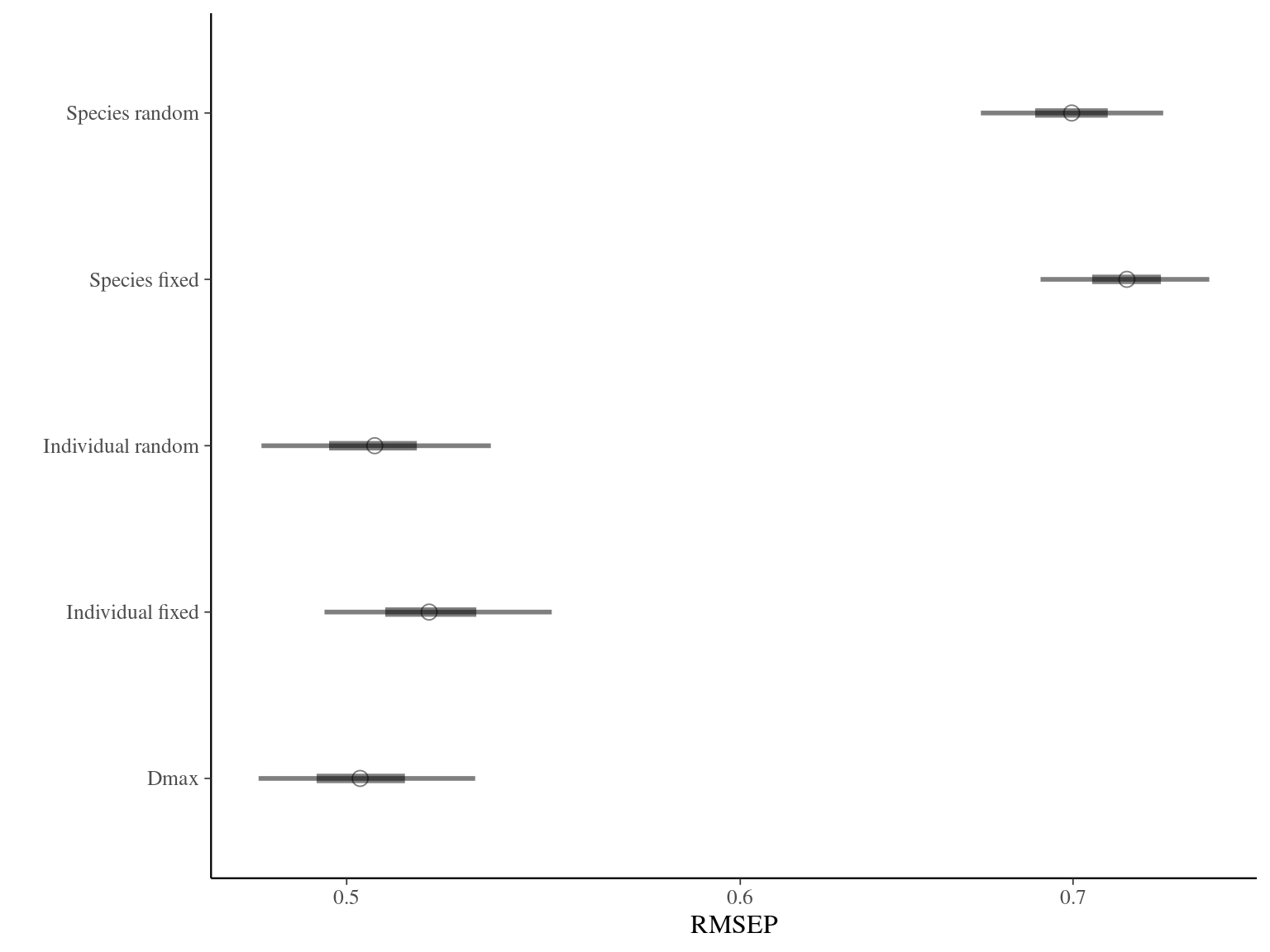
In this chapter, I looked for the best model to integrate species information based on quality of fit, cross-validation (LOO), and prediction (RMSEP). The result is summarised in Table 2.1.

2.1 Data

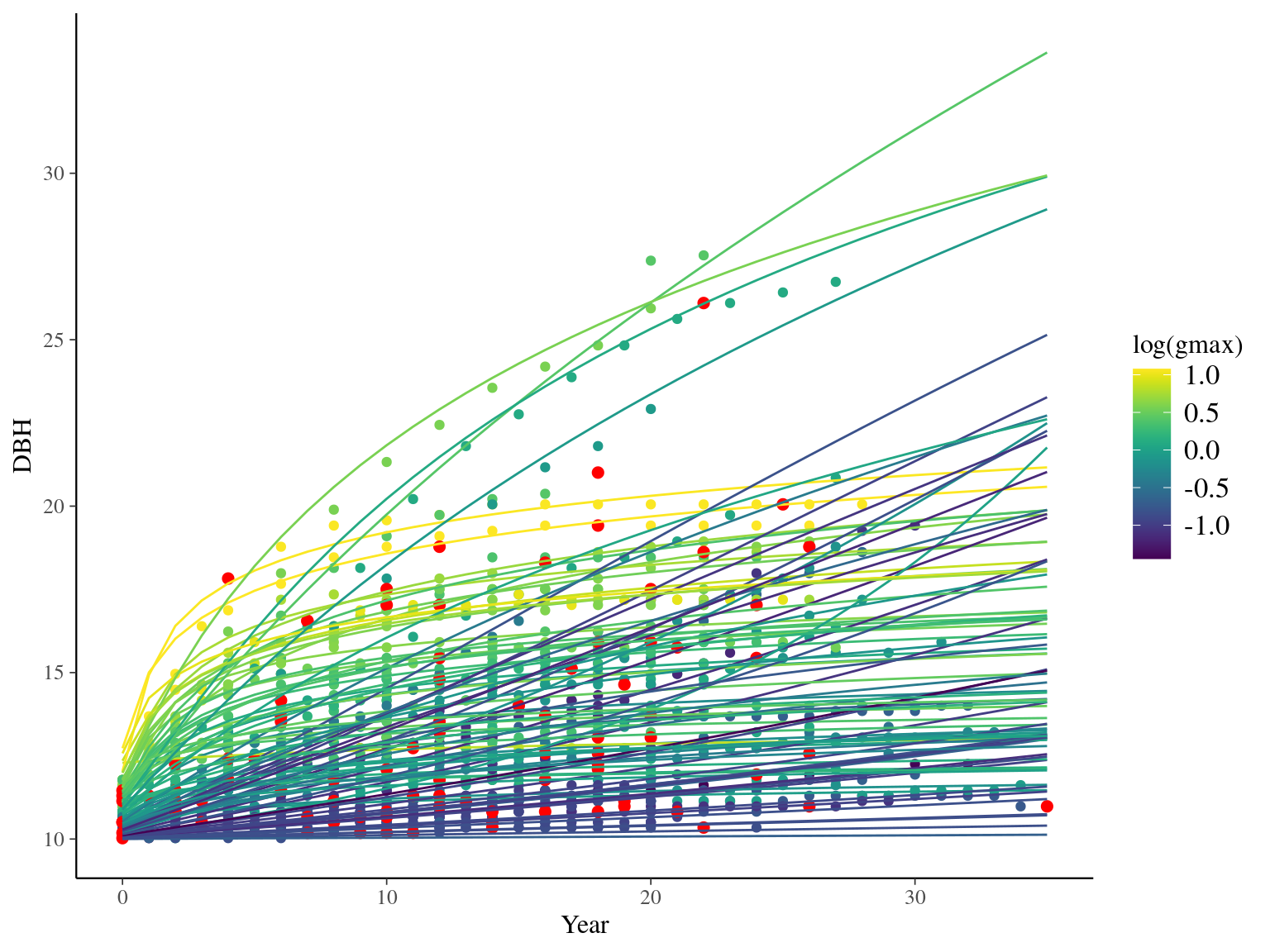
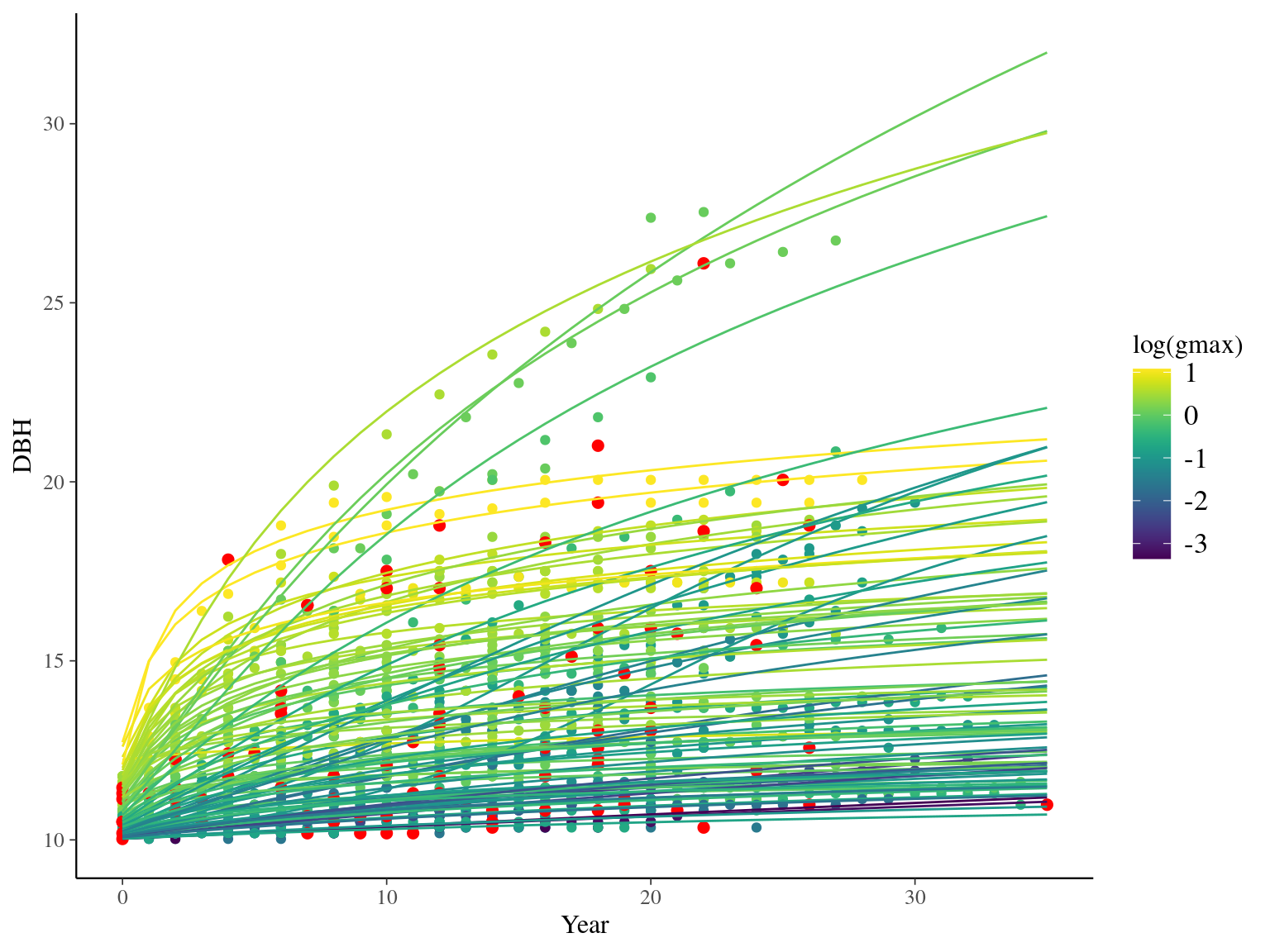
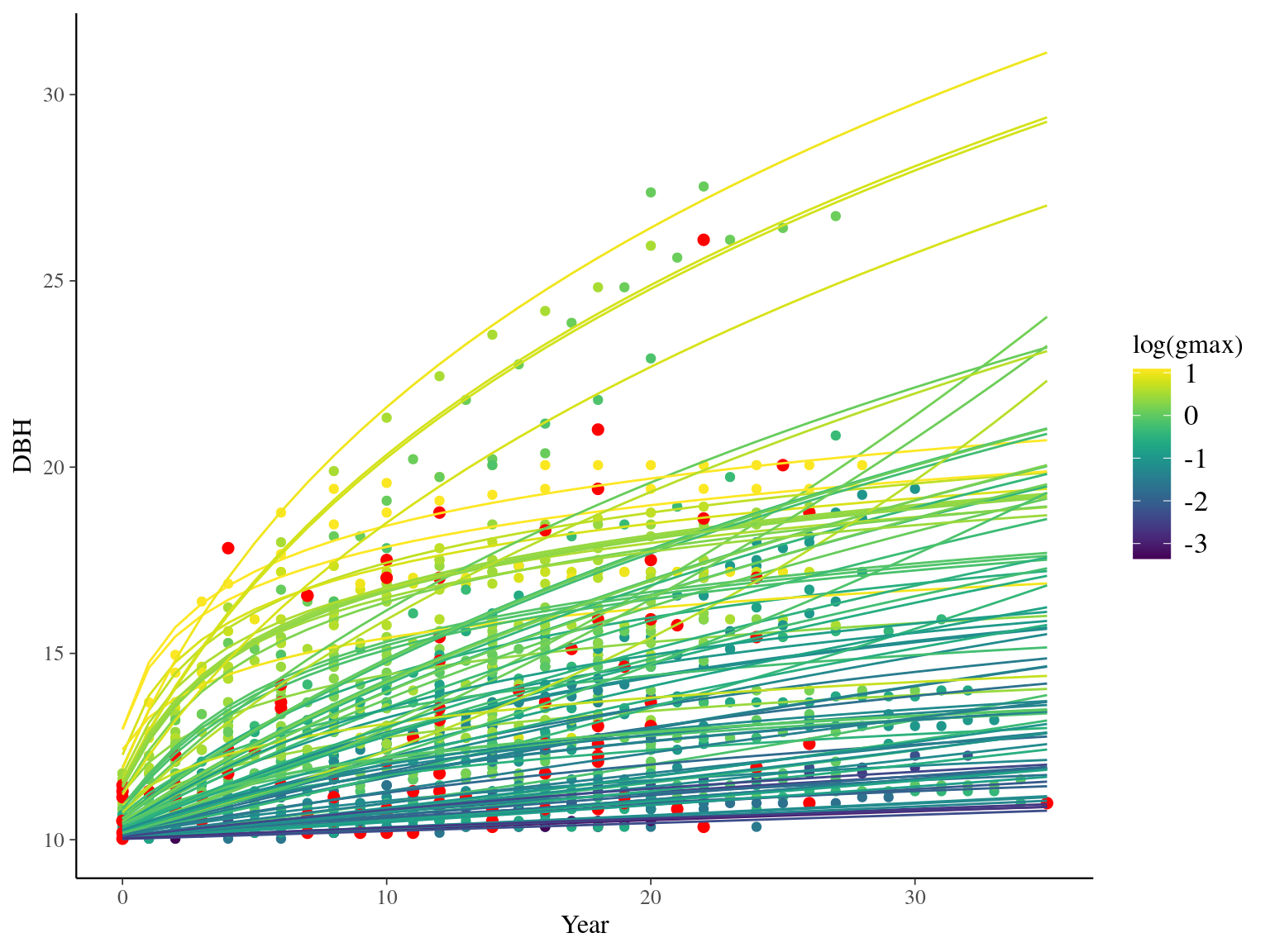
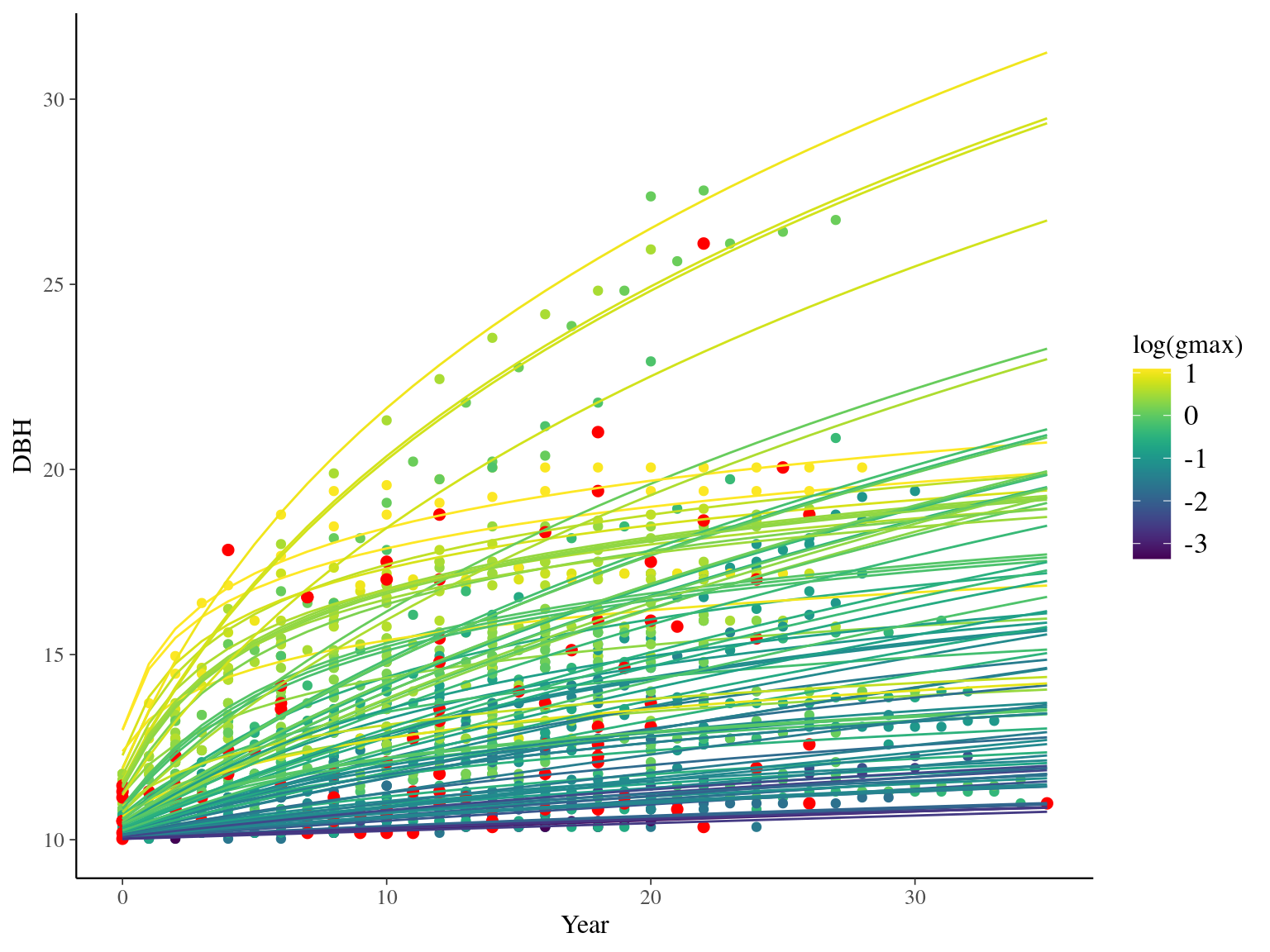
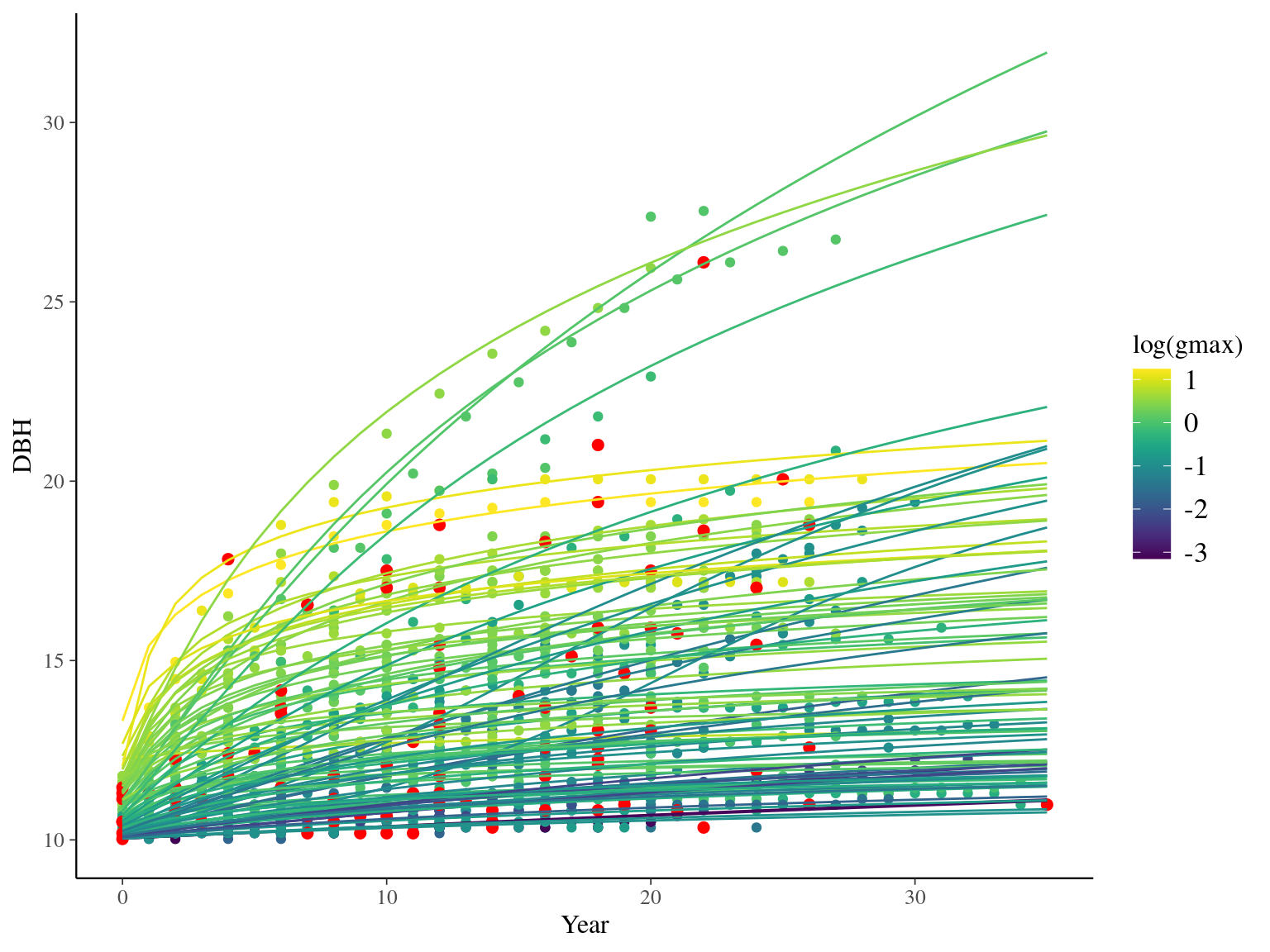
I used reduced data to explore the model form. I focused on trees at 20 meters from any plot edges for neighbourhood effect. I used only recruited trees in the censuses with at least 10 measurements of diameter at breast height (DBH, cm). I used only species with at least 10 trees following previous requirements. And, I randomly selected 10 trees among 9 species for lightweight training data. I further selected a random diameter measure for each individual as an evaluation data not used for model fitting (Fig. 2.1).

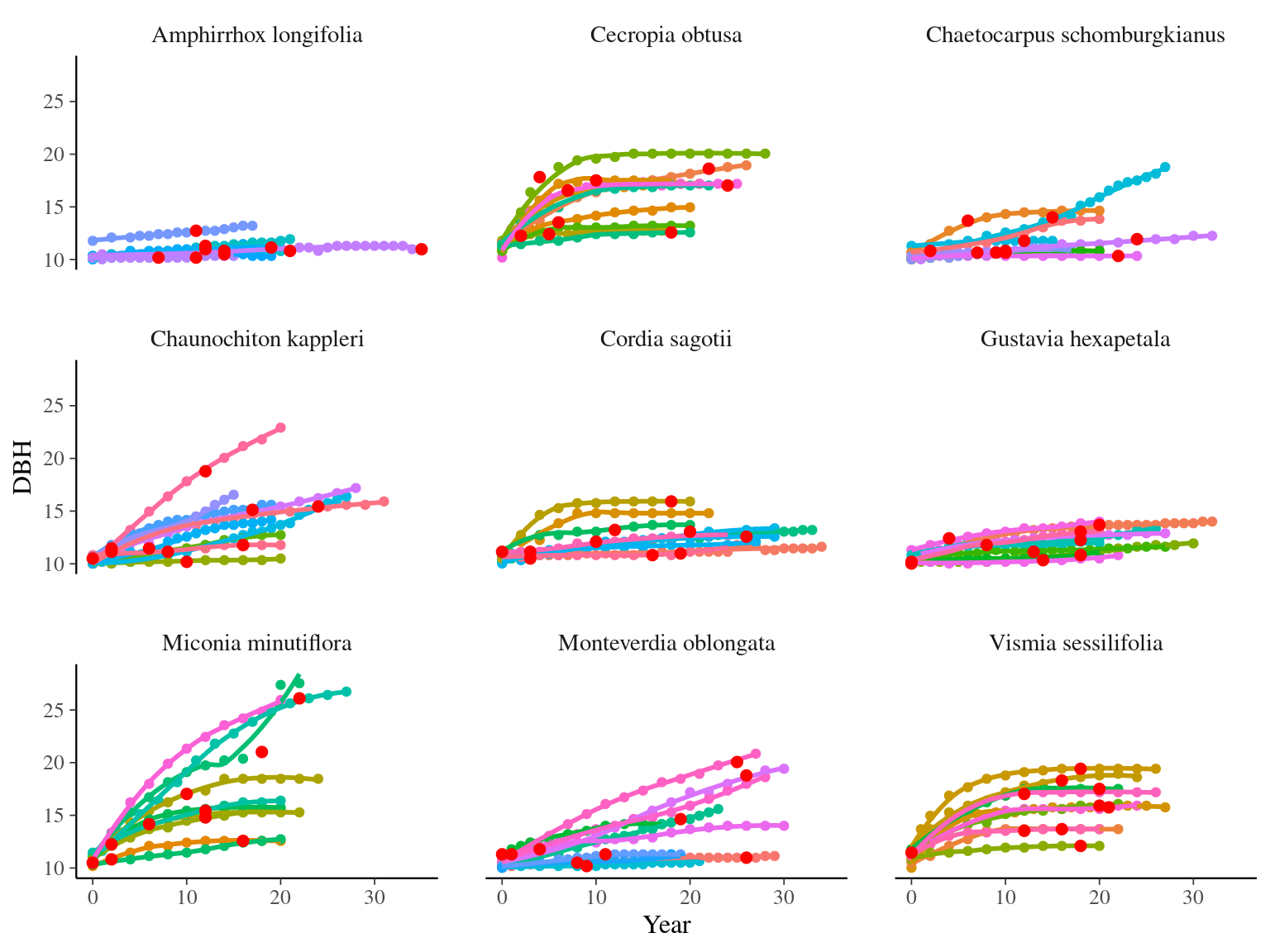
Figure 2.1: Tree diameter trajectories in training data. Color represent individuals and the red point the data used for evaluation.

2.2 Individual fixed

We used the selected model, i.e. Gompertz model (Herault2011?), with all parameters as individual fixed effects:

$$DBH_{t,i} \sim \mathcal N (10 + gmax_i \times \sum _{y=1|DBH_{t=0}} ^{y=t} exp(-\frac12.[\frac{log(\frac{DBH_{t,i}}{100.Dopt_i})}{Ks_i}]^2)), \sigma)$$

The model correctly converged ($\hat R < 1.05$) with an acceptable but marked correlation between $dopt$ and $ks$. $gmax$ posteriors have logical uncertainty but are varying widely among individuals. Finally predictions of the diameter trajectories by the model are good and realistic. Nevertheless, some posteriors seems to show bimodality.

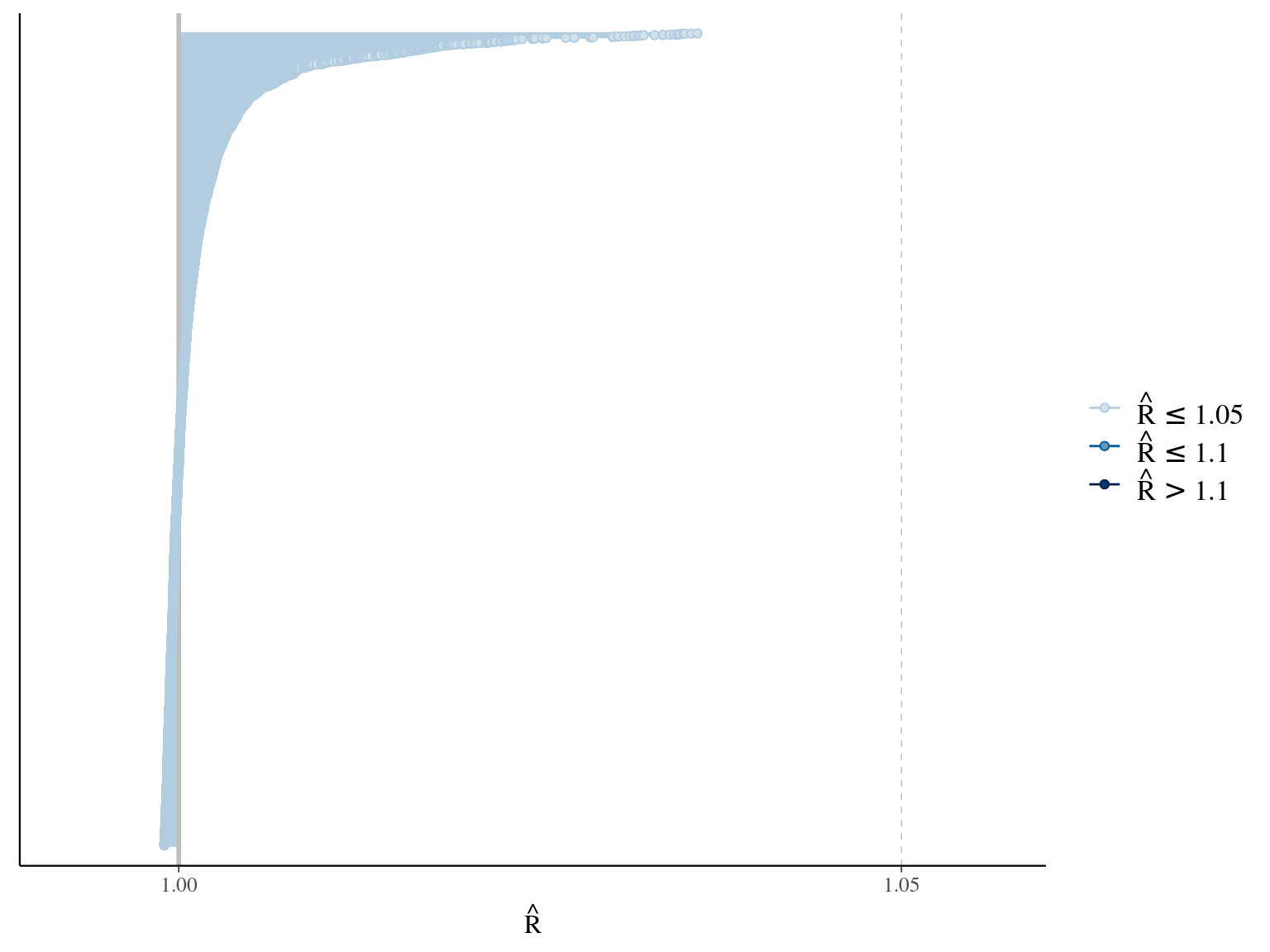
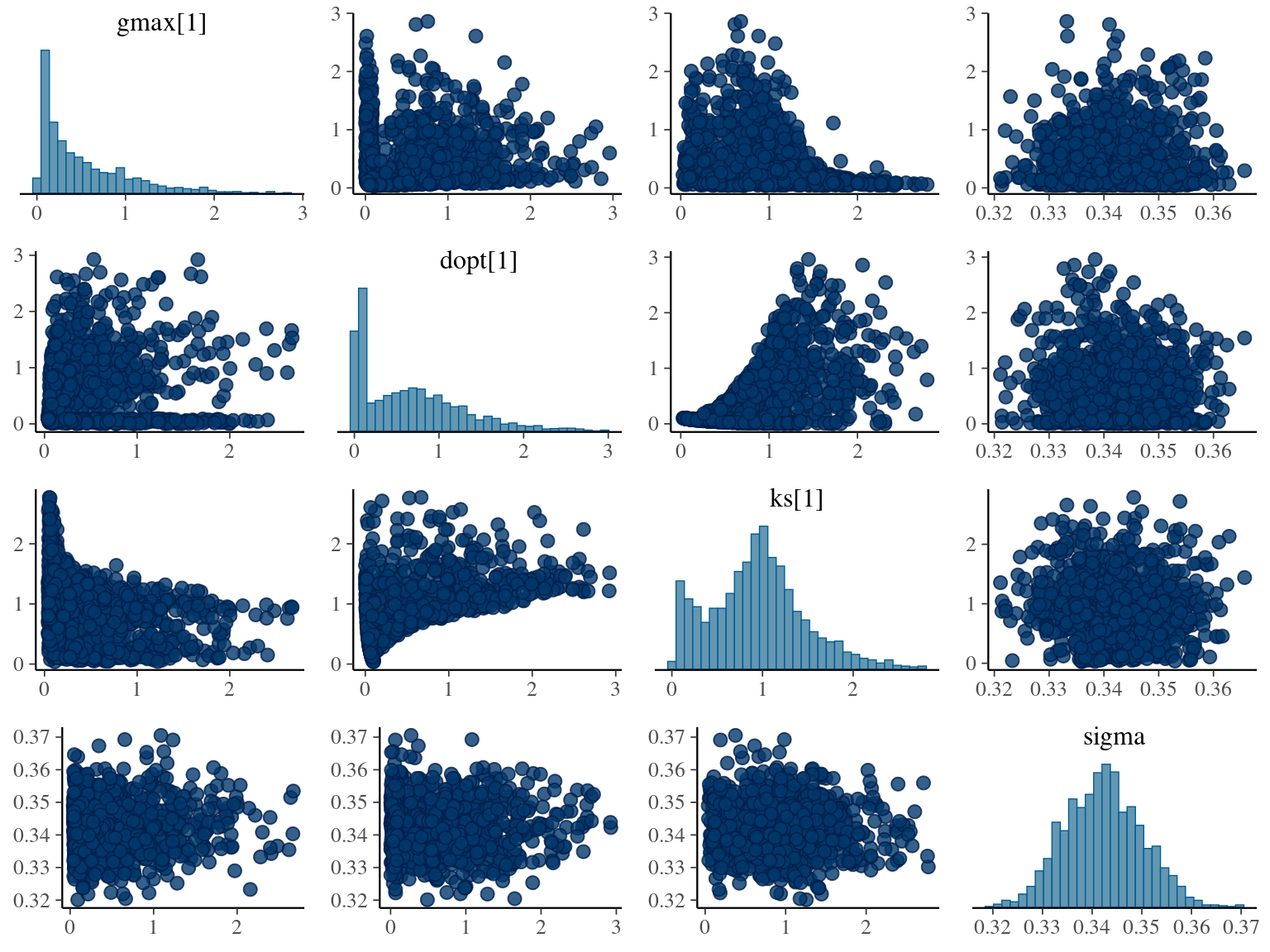
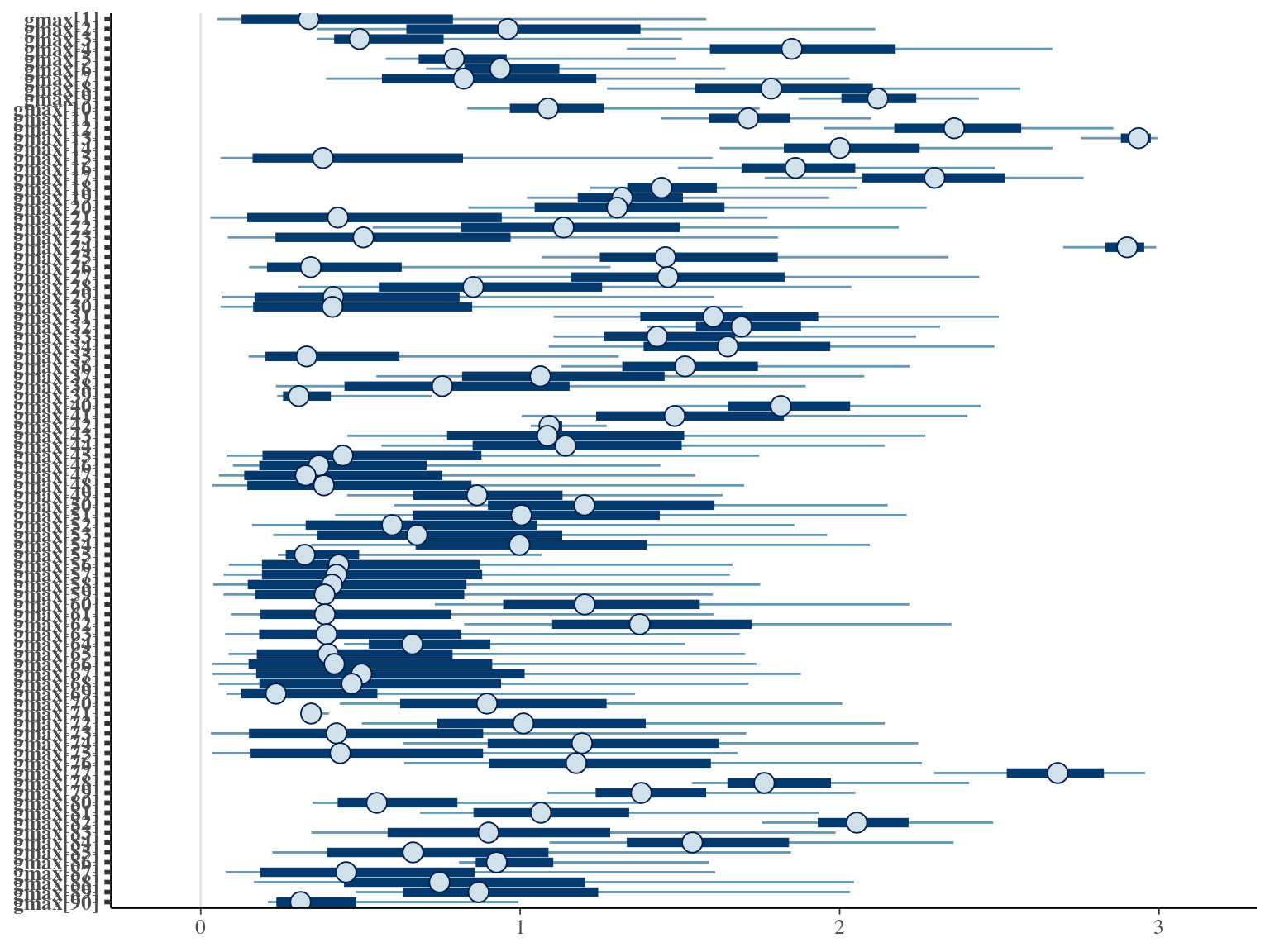
2.3 Individual random

We used the selected model, i.e. Gompertz model (Herault2011?), with $gmax$ as individual fixed effects and $Dopt$ and $Ks$ as individual random effects centered on species fixed effects:

$$DBH_{t,i,s} \sim \mathcal N (10 + gmax_i \times \sum _{y=1|DBH_{t=0}} ^{y=t} exp(-\frac12.[\frac{log(\frac{DBH_{t,i}}{100.Dopt_i})}{Ks_i}]^2)), \sigma) \\| Dopt_i \sim \mathcal N(Dopt_s,\sigma_D), Ks_i \sim \mathcal N(Ks_s,\sigma_K)$$

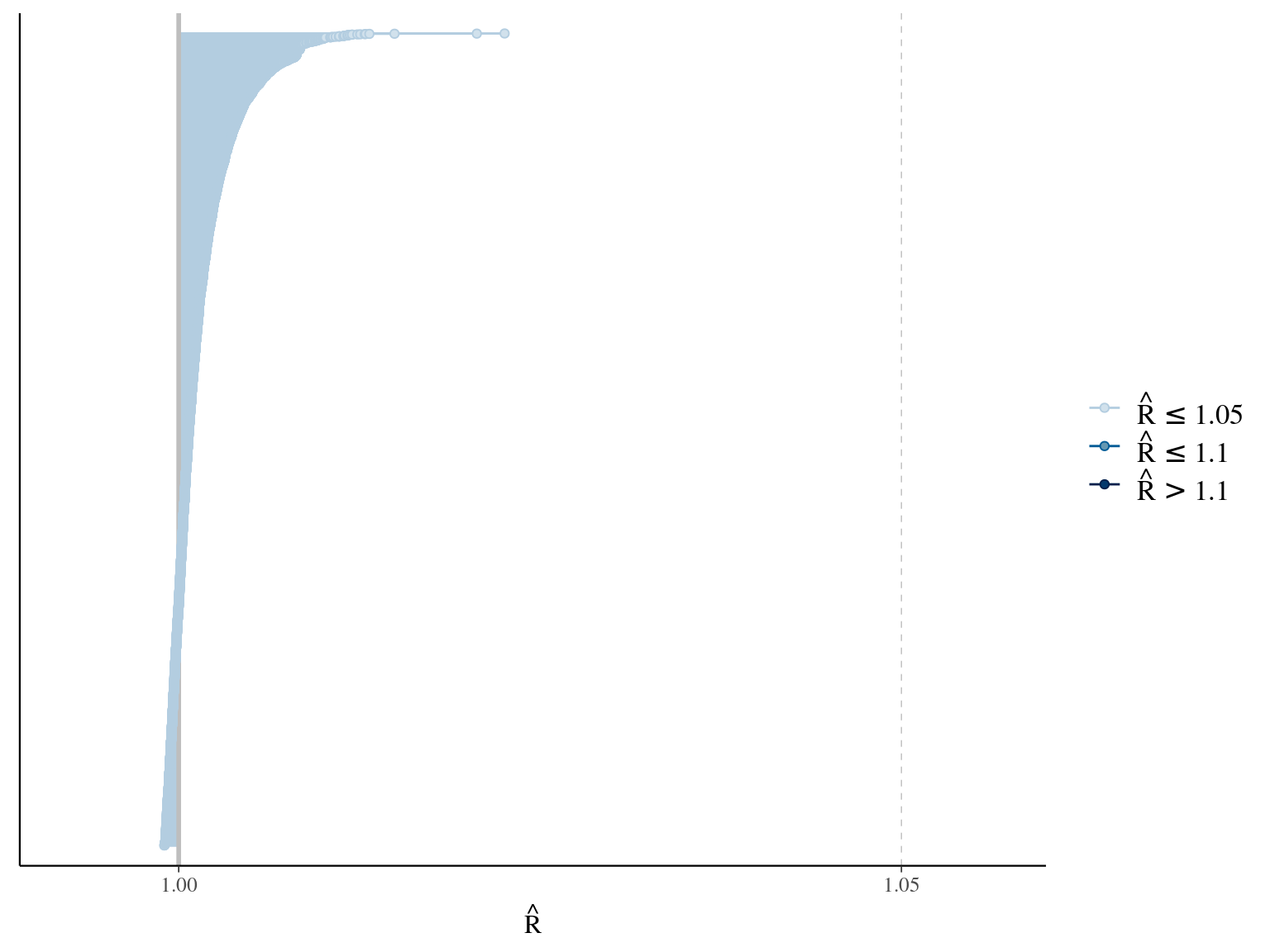
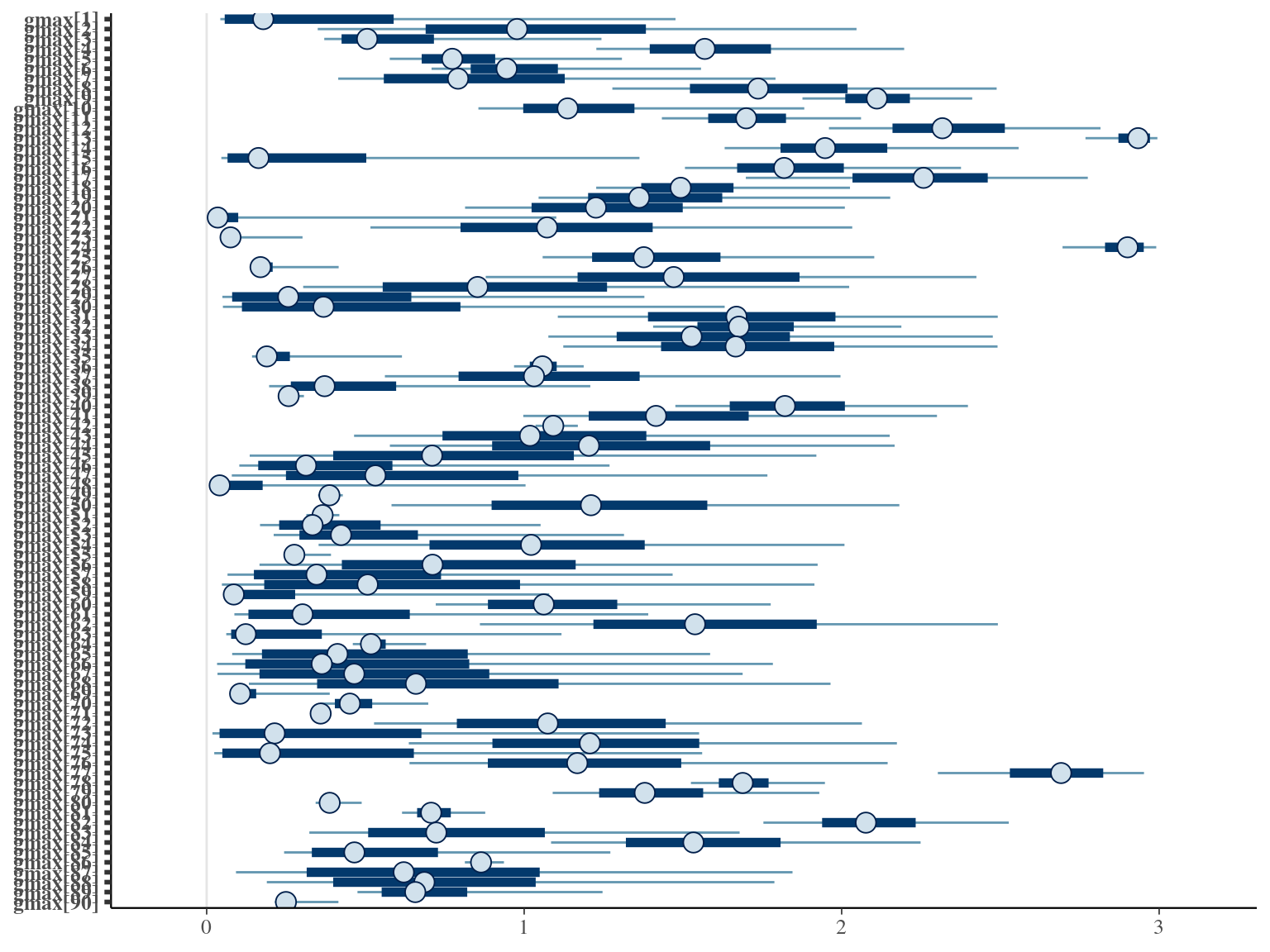
The model correctly converged ($\hat R < 1.05$) with an acceptable but marked correlation between $dopt$ and $ks$. $gmax$ posteriors have logical uncertainty but are varying widely among individuals. Finally predictions of the diameter trajectories by the model are good and realistic.

2.4 Species fixed

We used the selected model, i.e. Gompertz model (Herault2011?), with $gmax$ as individual fixed effects and $Dopt$ and $Ks$ as species fixed effects:

$$DBH_{t,i,s} \sim \mathcal N (10 + gmax_i \times \sum _{y=1|DBH_{t=0}} ^{y=t} exp(-\frac12.[\frac{log(\frac{DBH_{t,i}}{100.Dopt_s})}{Ks_s}]^2)), \sigma)$$

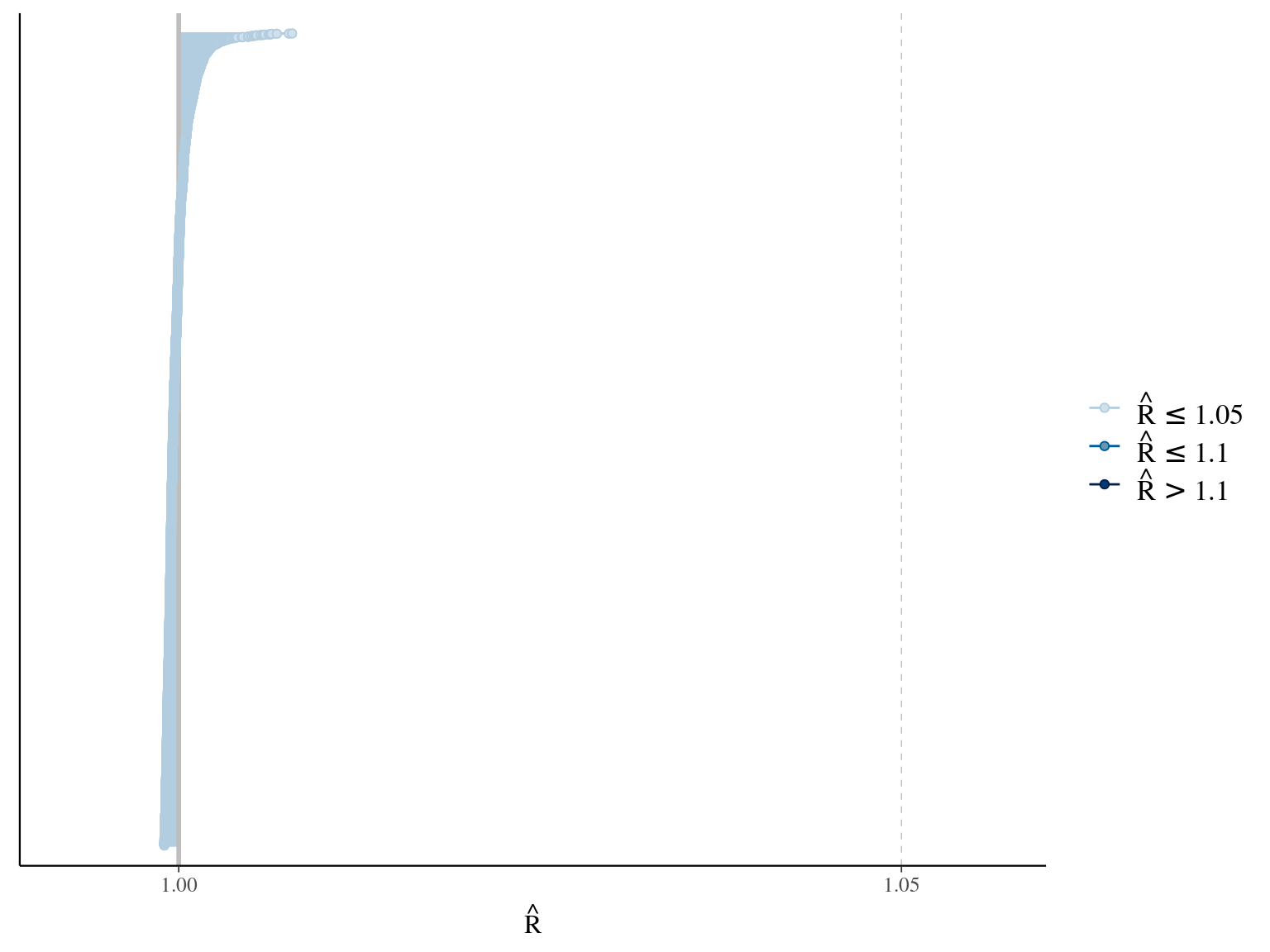
The model correctly converged ($\hat R < 1.05$) with an acceptable but marked correlation between $dopt$ and $ks$. $gmax$ posteriors have logical uncertainty but are varying widely among individuals. Finally predictions of the diameter trajectories by the model are good and realistic.

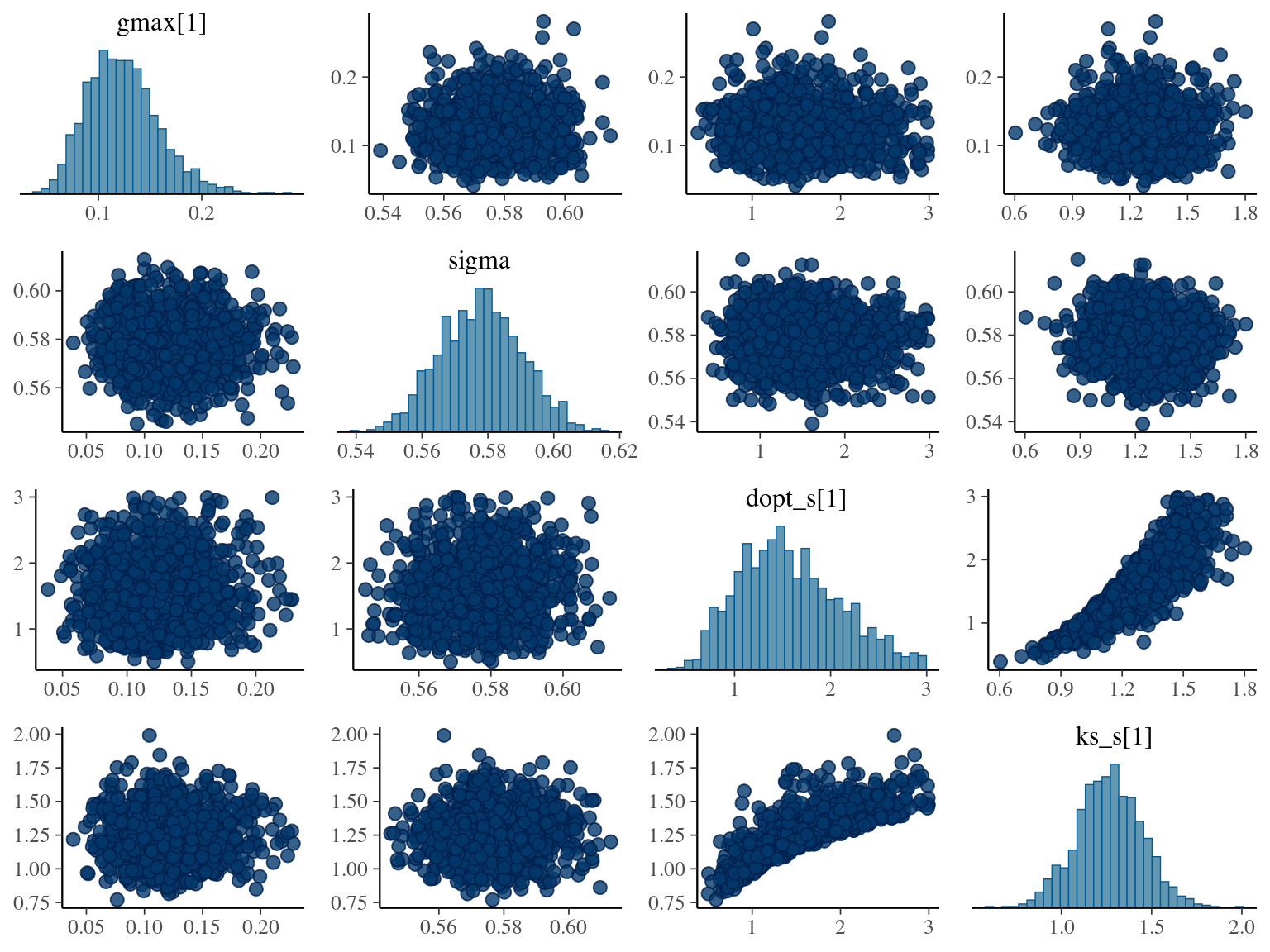
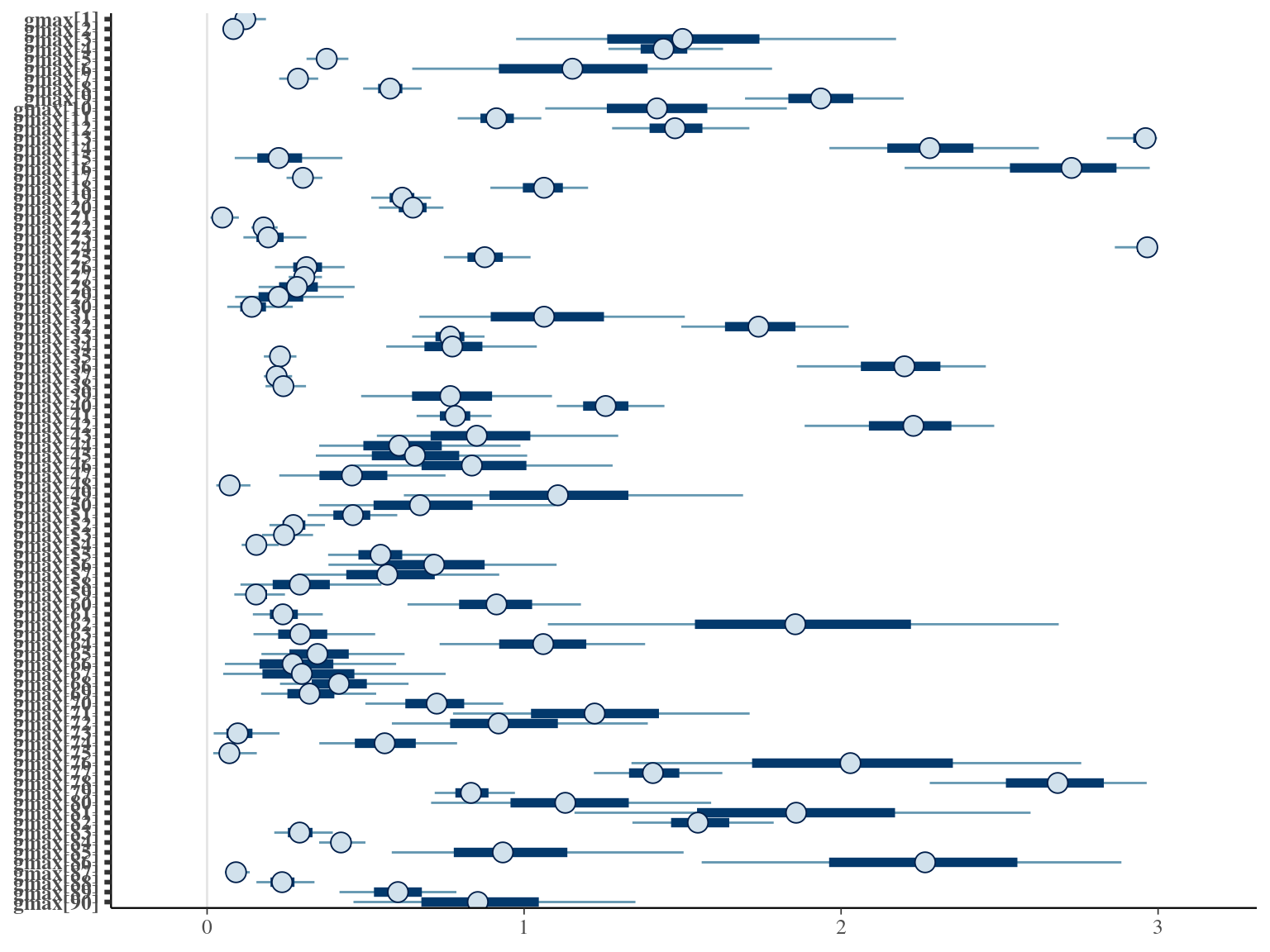
2.5 Species random

We used the selected model, i.e. Gompertz model (Herault2011?), with $gmax$ as individual fixed effects and $Dopt$ and $Ks$ as species random effects centered on community fixed effects:

$$DBH_{t,i,s} \sim \mathcal N (10 + gmax_i \times \sum _{y=1|DBH_{t=0}} ^{y=t} exp(-\frac12.[\frac{log(\frac{DBH_{t,i}}{100.Dopt_s})}{Ks_s}]^2)), \sigma) \\| Dopt_i \sim \mathcal N(Dopt,\sigma_K), Ks \sim \mathcal N(Ks,\sigma_D)$$

The model correctly converged ($\hat R < 1.05$) with an acceptable but marked correlation between $dopt$ and $ks$. $gmax$ posteriors have logical uncertainty but are varying widely among individuals. Finally predictions of the diameter trajectories by the model are good and realistic.

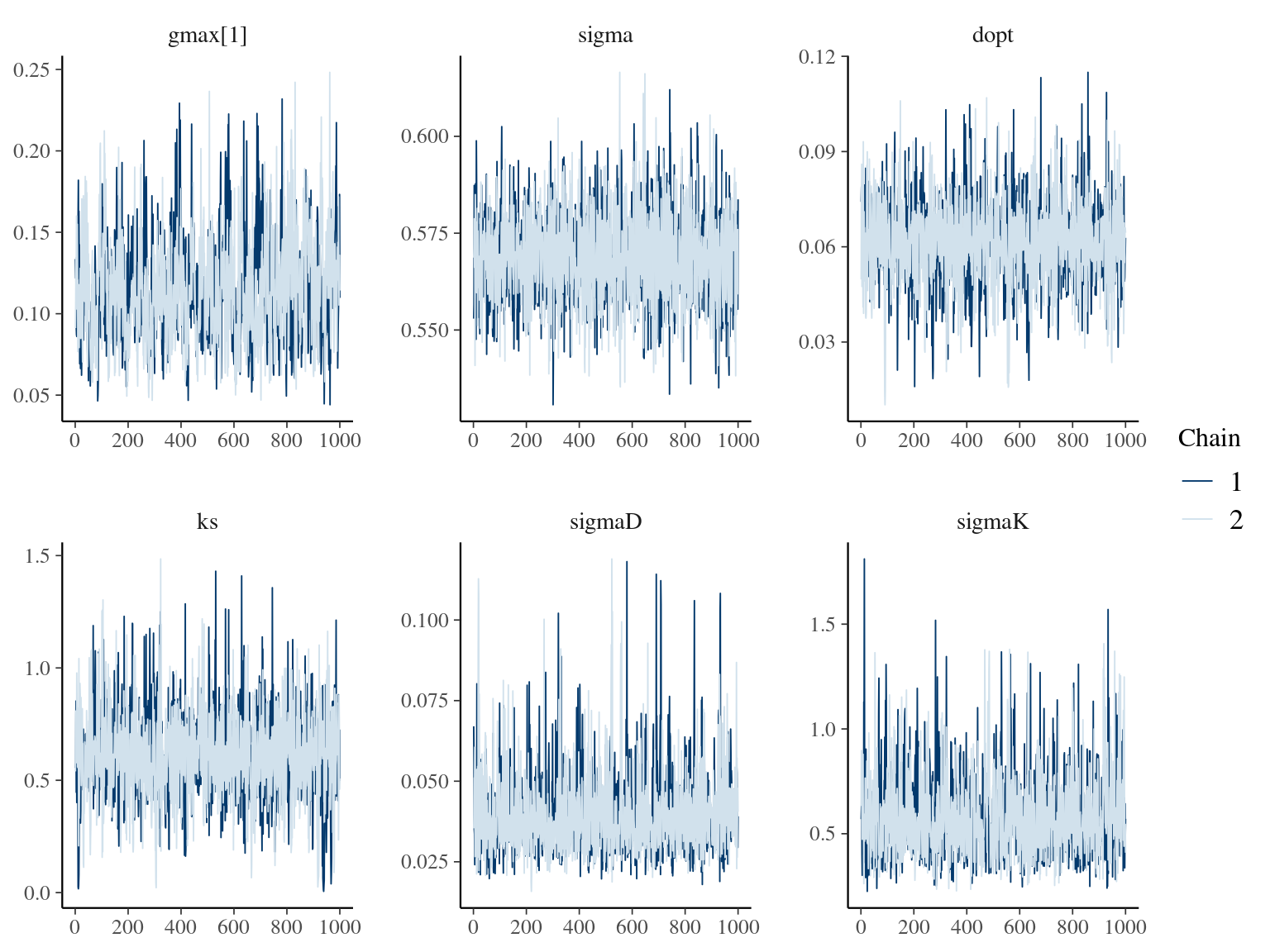
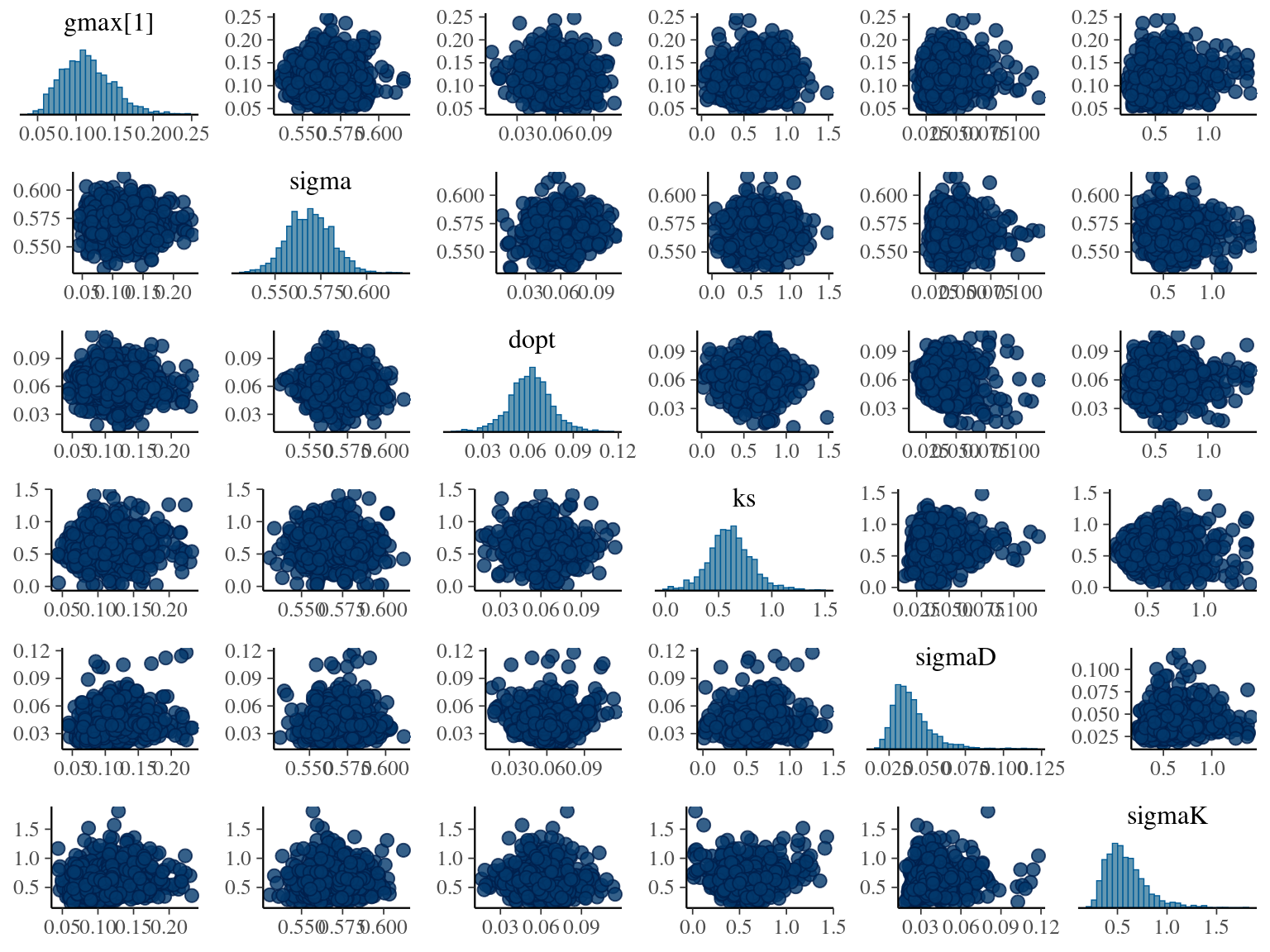
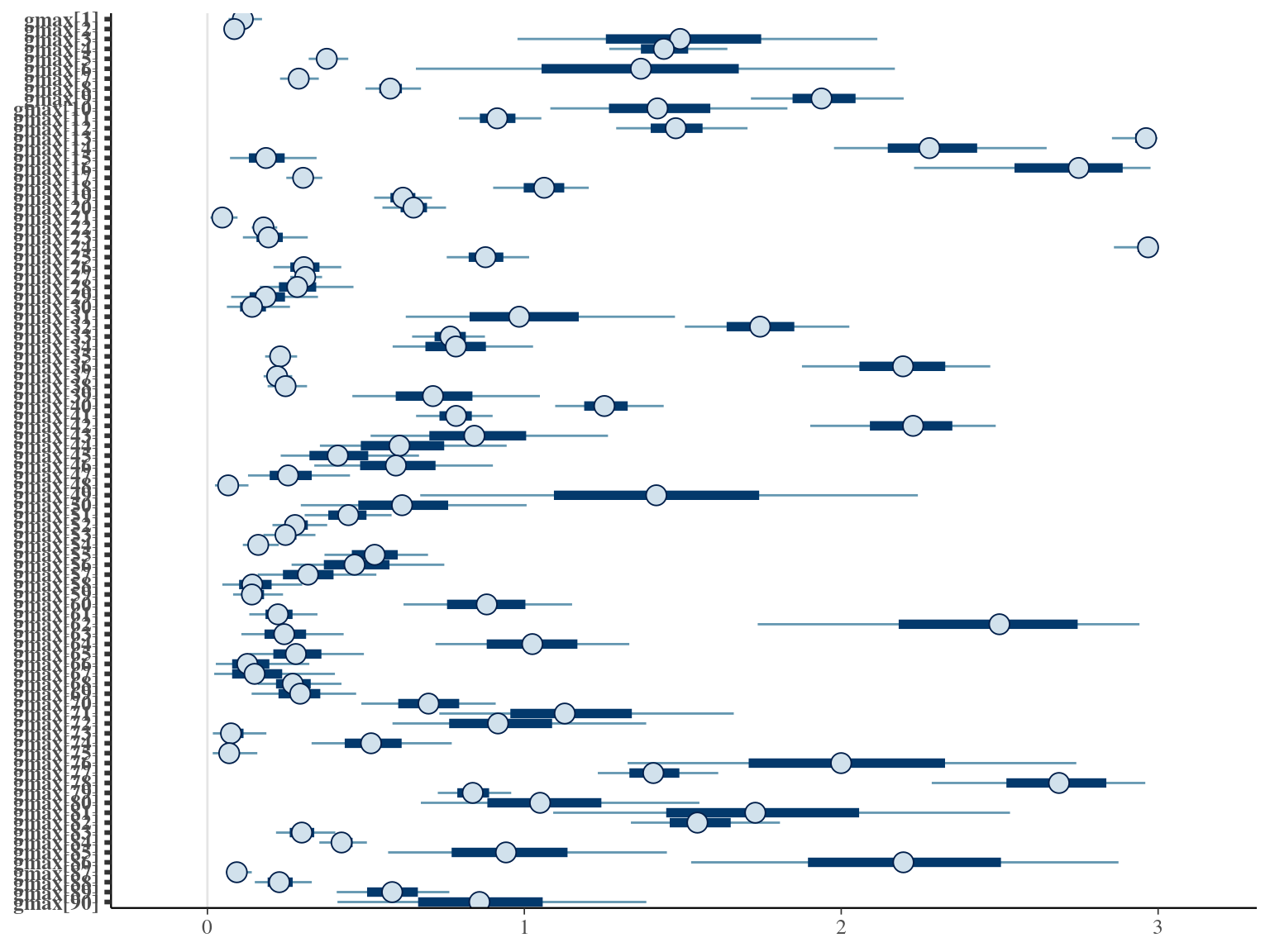
2.6 Dmax

We used the selected model, i.e. Gompertz model (Herault2011?), with $gmax$ as individual fixed effects and $Dopt$ and $Ks$ as individual random effects centered on species fixed effects:

$$DBH_{t,i,s} \sim \mathcal N (10 + gmax_i \times \sum _{y=1|DBH_{t=0}} ^{y=t} exp(-\frac12.[\frac{log(\frac{DBH_{t,i}}{100.Dopt_i})}{Ks_i}]^2)), \sigma) \\| Dopt_i \sim \mathcal N(Dopt_s,\sigma_D), Ks_i \sim \mathcal N(Ks_s,\sigma_K)$$

But we constrained $dopt$ fitting $d=\frac{dopt}{DBH_{95}}$ with $d\in[0,1]$. The model correctly converged ($\hat R < 1.05$) with an acceptable but marked correlation between $dopt$ and $ks$. $gmax$ posteriors have logical uncertainty but are varying widely among individuals. Finally predictions of the diameter trajectories by the model are good and realistic.

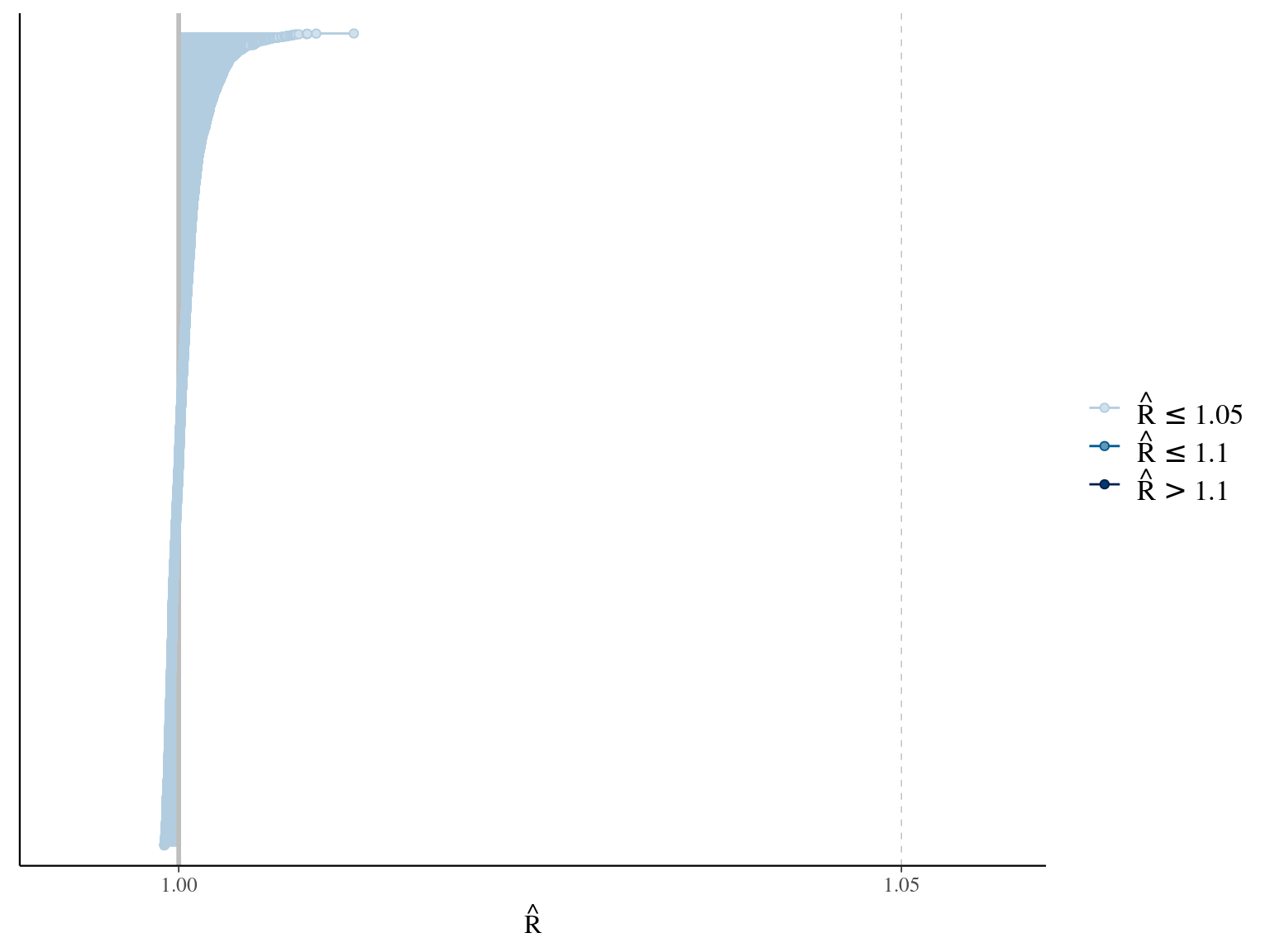
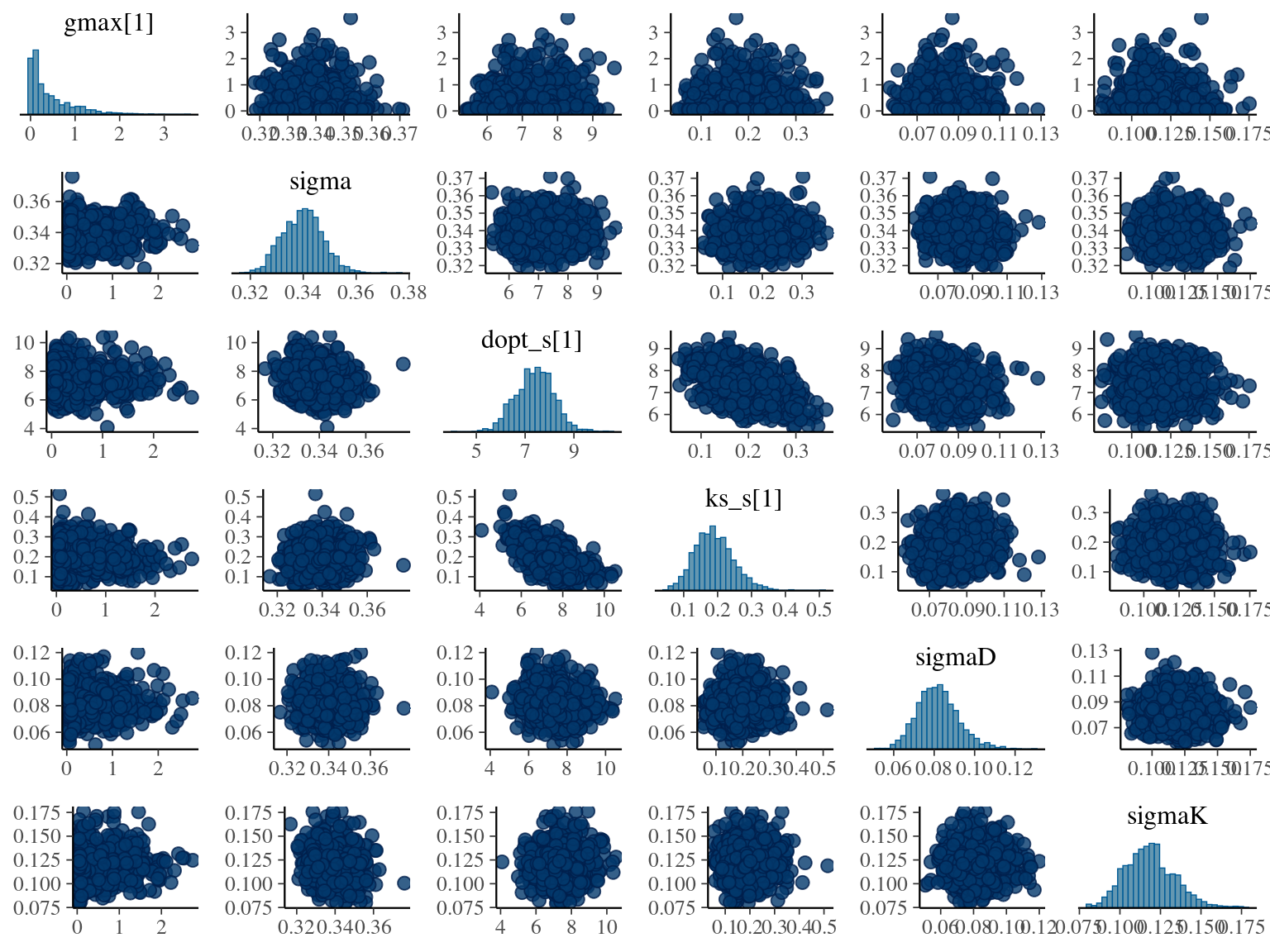
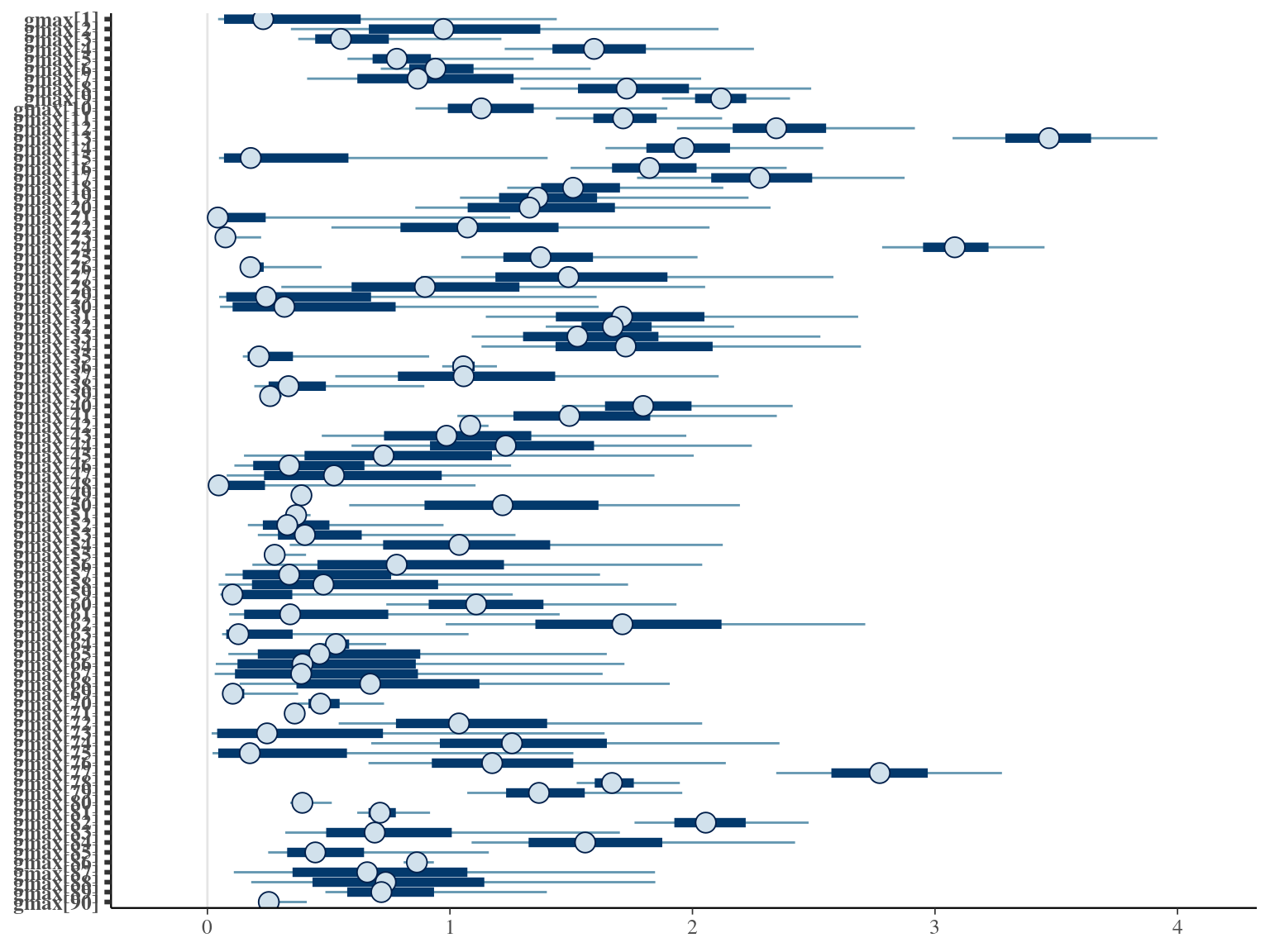
2.7 Comparisons

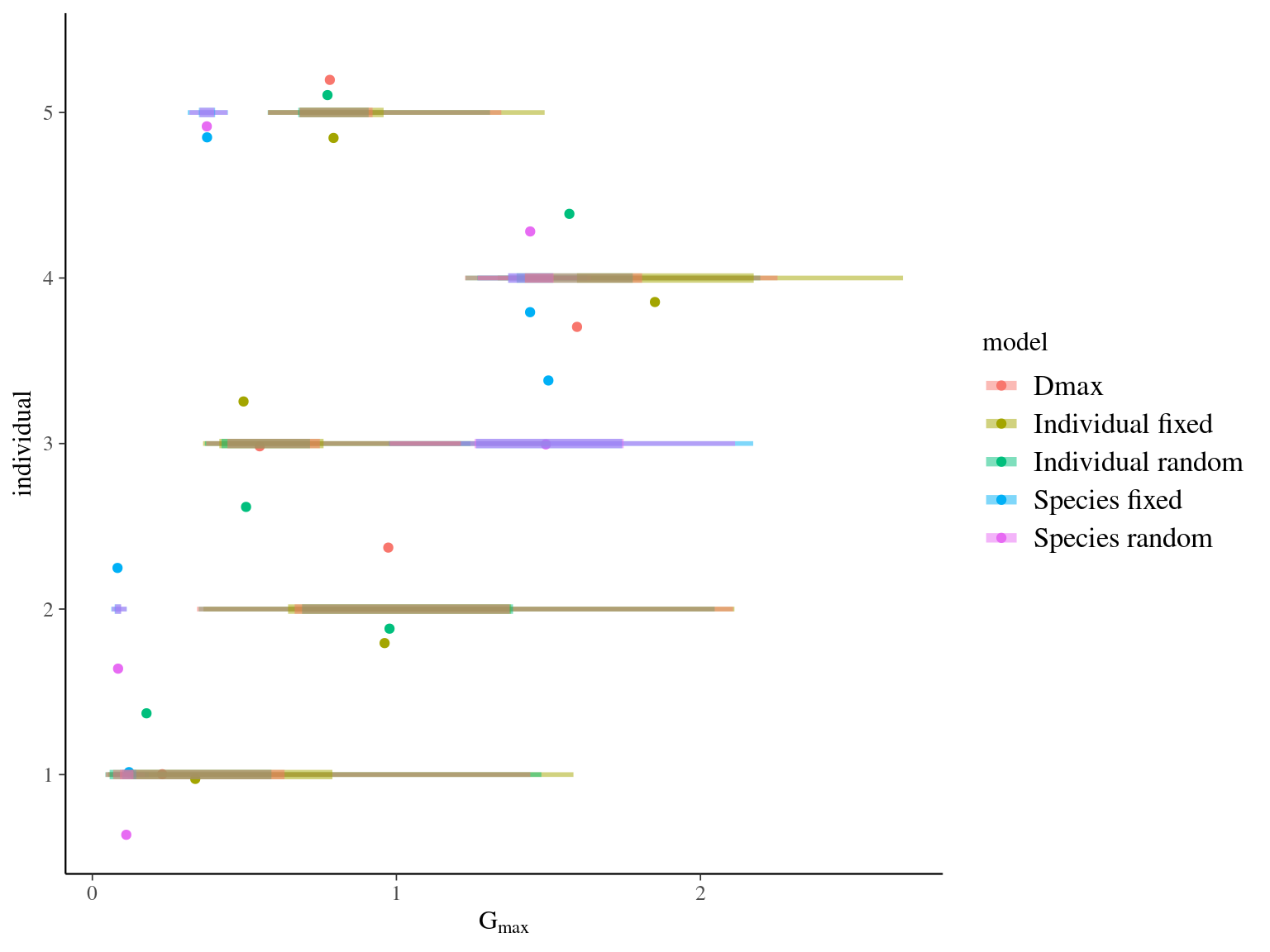
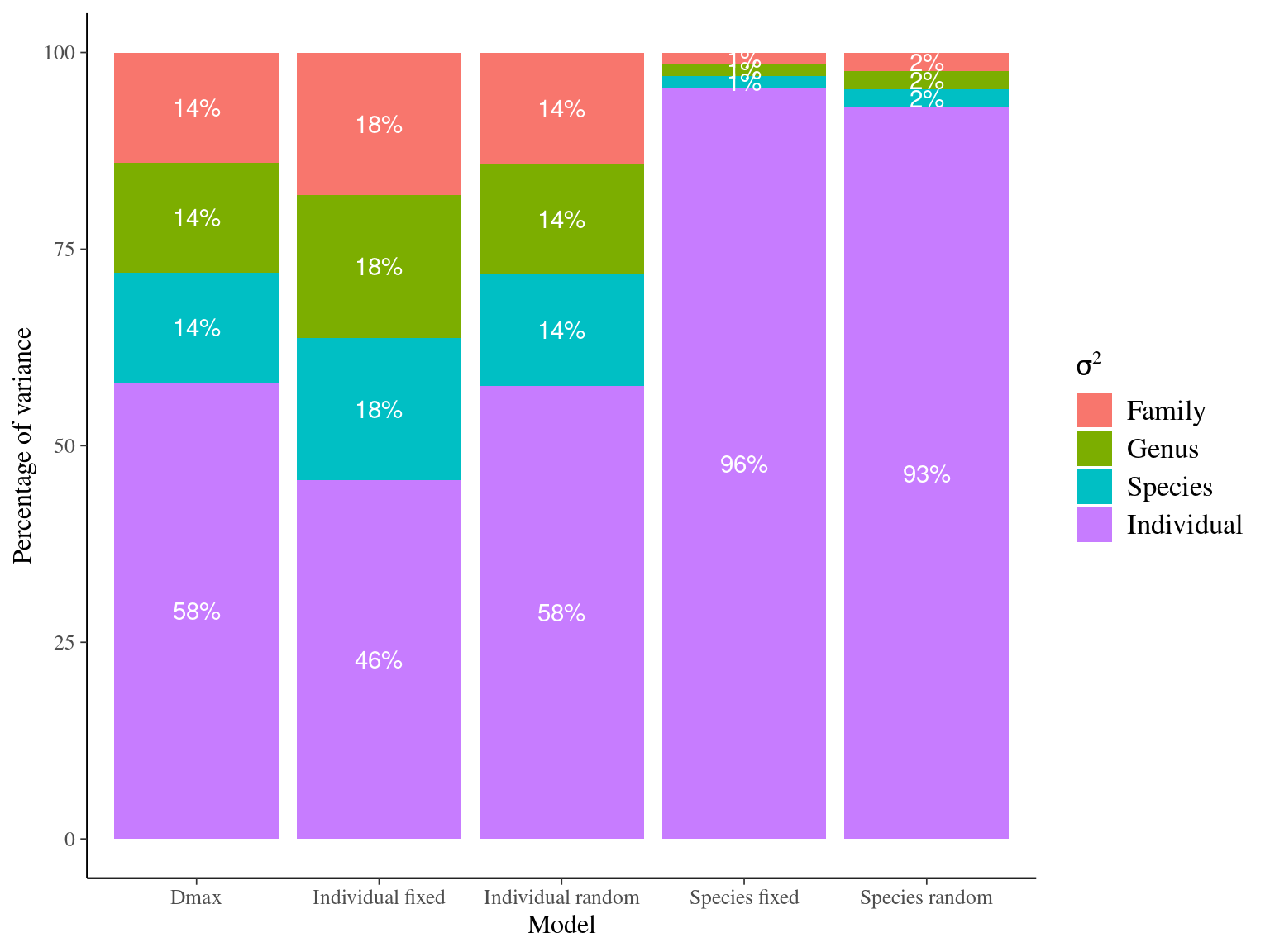
The individual random model has the best prediction (lowest RMSEP) associated to the best evaluation (second lowest loo epld), and a decent computing time. Moreover, model using species level $Dopt$ and $Ks$ are underestimating $Gmax$ absolute value while overestimating individual variation in $Gmax$ (last figures). Moreover, constraining $dopt$ fitting $d=\frac{dopt}{DBH_{95}}$ with $d\in[0,1]$ resolved maximum treedepth issues and have similar performances. This is the best model that I’ll use in next steps.

Table 2.1: Model choice summary with quality of prediciton (Root Mean Square Error of Prediction, RMSEP), cross-validation (Leave-One-Out Estimate of the expected Log pointwise Predictive Density, LOO ELDP), and speed (Elapsed yime).

Model	RMSEP	LOO ELDP	Elapsed time
Individual fixed	0.5194675	-519.5235	1098.084
Individual random	0.5065365	-511.3851	467.245
Species fixed	0.7176675	-1131.3198	297.436
Species random	0.6995610	-1113.3024	405.419
Dmax	0.5031310	-511.7936	495.079

	elpd_diff	se_diff	elpd_loo	se_elpd_loo	p_loo	se_p_loo	looic	se_looic
Individual random	0.0000000	0.000000	-511.3851	66.12526	141.06429	19.340438	1022.770	132.25052
Dmax	-0.4085308	5.008777	-511.7936	67.24839	148.77584	20.302966	1023.587	134.49677
Individual fixed	-8.1383963	8.967316	-519.5235	63.32304	144.10479	17.511319	1039.047	126.64607
Species random	-601.9172862	50.741055	-1113.3024	38.22549	91.71500	8.904312	2226.605	76.45097
Species fixed	-619.9346413	51.696773	-1131.3198	37.95275	89.35234	8.624910	2262.640	75.90549