This book is in Open Review. I want your feedback to make the book better for you and other readers. To add your annotation, select some text and then click the on the pop-up menu. To see the annotations of others, click the in the upper right hand corner of the page

Chapter 3 Model half

In this chapter, I fitted the selected model with reduced data.

3.1 Data

I focused on trees at 20 meters from any plot edges for neighbourhood effect. I used only recruited trees in the censuses with at least 10 measurements of diameter at breast height (DBH, cm). I used only species with at least 10 trees following previous requirements. And, I randomly selected 20 trees in each species (Tab. 3.1 & Fig. 3.1).

Table 3.1: Metrics on inventory data used to fit the full model including sample size (N), memdian, minimum and maximum values for families, genera, species, individuals, observations, cenusus, recruitment year (year0), last censused year (yearmax), recruitment diameter (dbh0) and last censused diameter (dbhmax).

	N	Median	Minimum	Maximum
families	38
genera	95
species	138
individuals	1 995
observations	30 432
census		14	11	30
year0		1 997	1 985	2 010
yearmax		2 019	2 003	2 021
dbh0		11	5	15
dbhmax		15	6	77

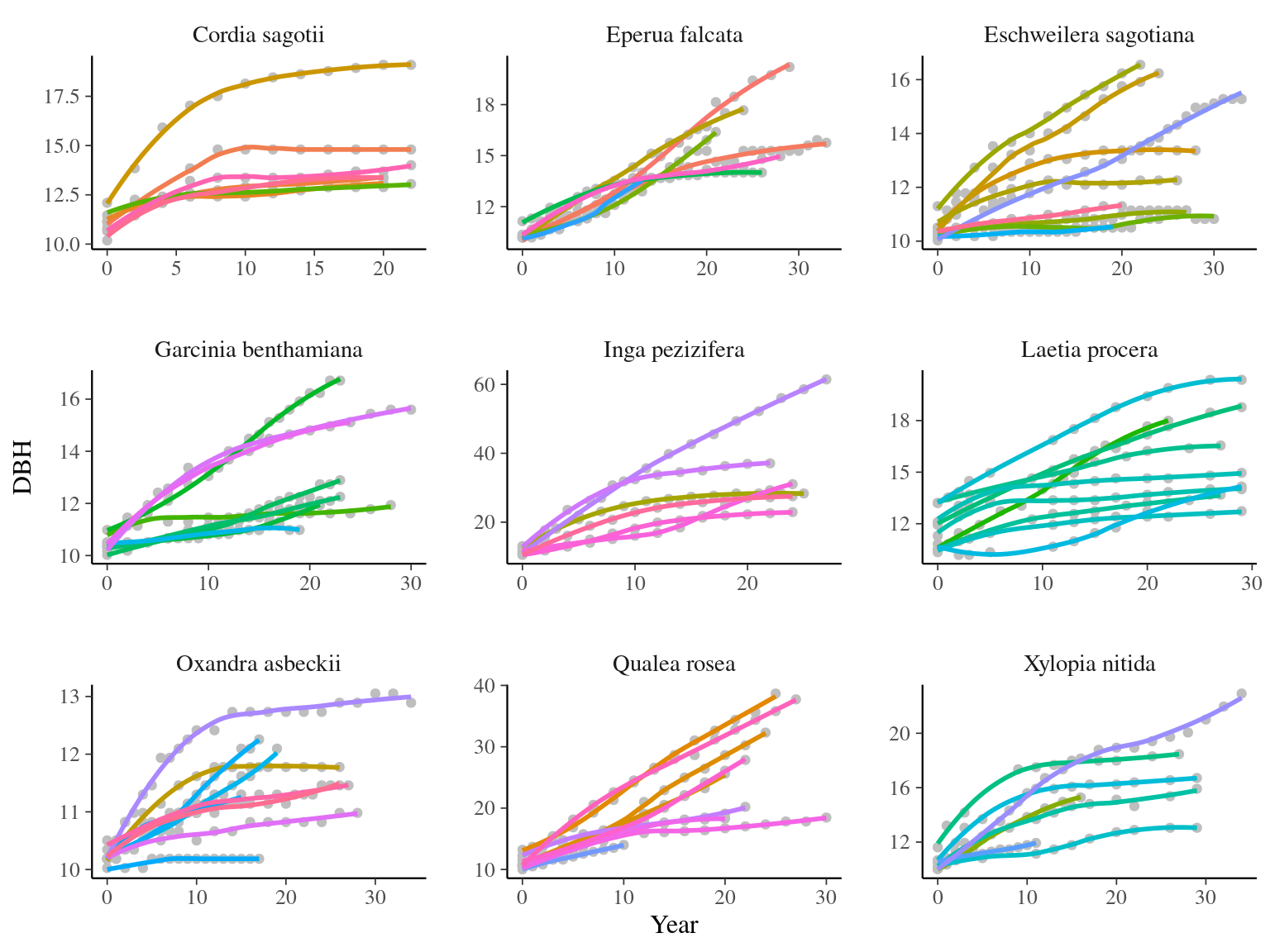
Figure 3.1: Tree diameter trajectories in reduced data. Color represent individuals.

3.2 Model

I used a Gompertz model (Hérault et al. 2011), were the diameter of individual \(i\) at year \(t\) is the sum of annual growth from \(t0\) to \(t\):

\[ DBH_{t,i,s} \sim \mathcal N (10 + Gmax_i \times \sum _{y=1|DBH_{t=0}} ^{y=t} exp(-\frac12.[\frac{log(\frac{DBH_{t,i}}{100.Dopt_i})}{Ks_i}]^2)), \sigma) \\| Dopt_i \sim \mathcal N(Dopt_s,\sigma_D), Ks_i \sim \mathcal N(Ks_s,\sigma_K) \]

The annual growth rate for individual \(i\) at year \(y\) with a diameter of \(DBH_{y,i}\) is defined following a Gompertz model (Gompertz 1825) already identified as the best model for growth-trajectories in Paracou (Hérault et al. 2011), where \(Gmax_i\) is the fixed maximum growth potential of every individual, \(Dopt_i\) is the optimal diameter at which the individual reaches its maximum growth potential, and \(Ks_i\) is the kurtosis defining the width of the bell-shaped growth-trajectory (see figure 1 in Hérault et al. 2011). \(Dopt_i\) and \(Ks_i\) are random effects centered on species parameters \(Dopt_s\) and \(Ks_s\) with associated variances \(\sigma_D\) and \(\sigma_K\).

3.3 Fit

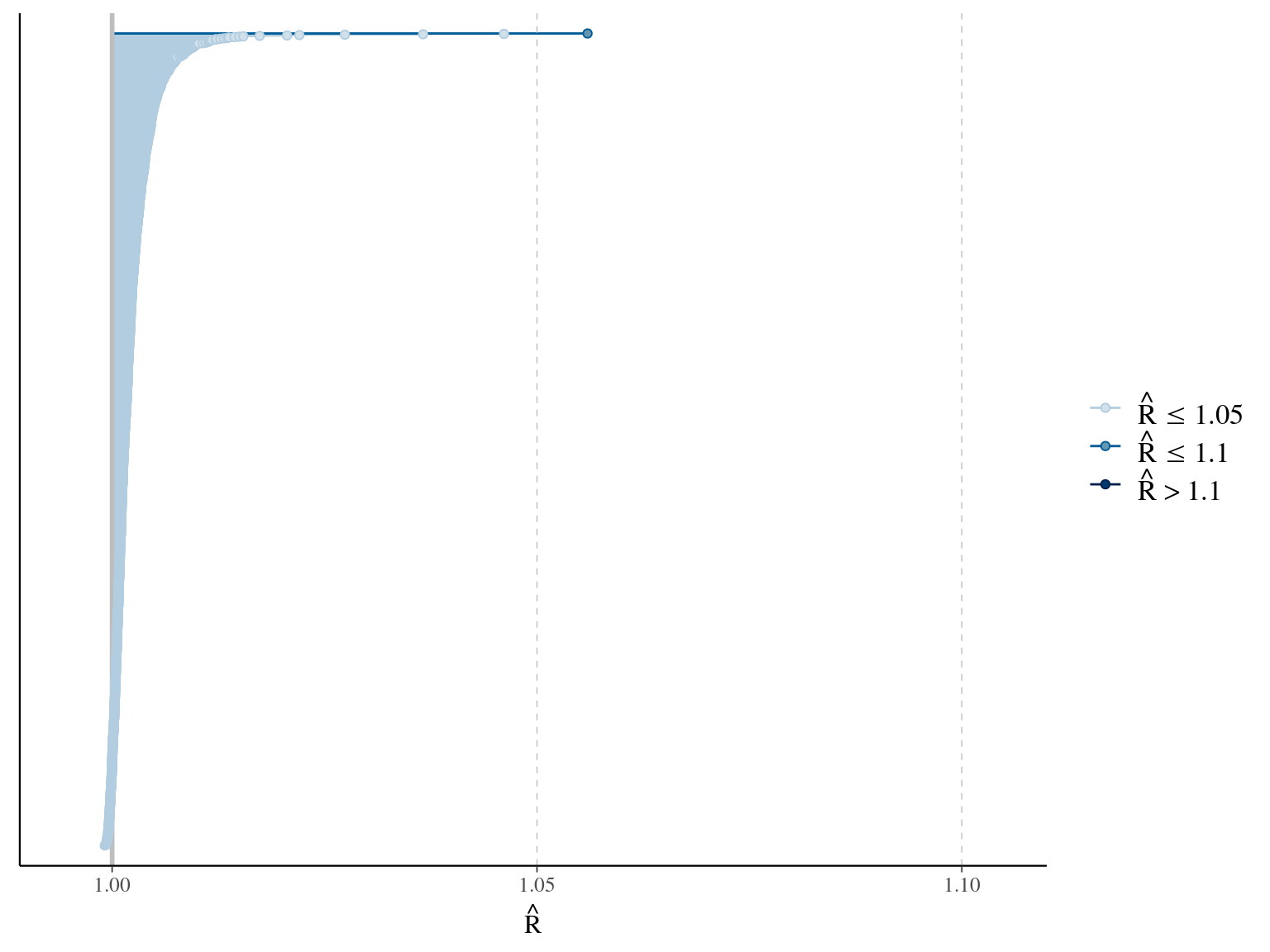
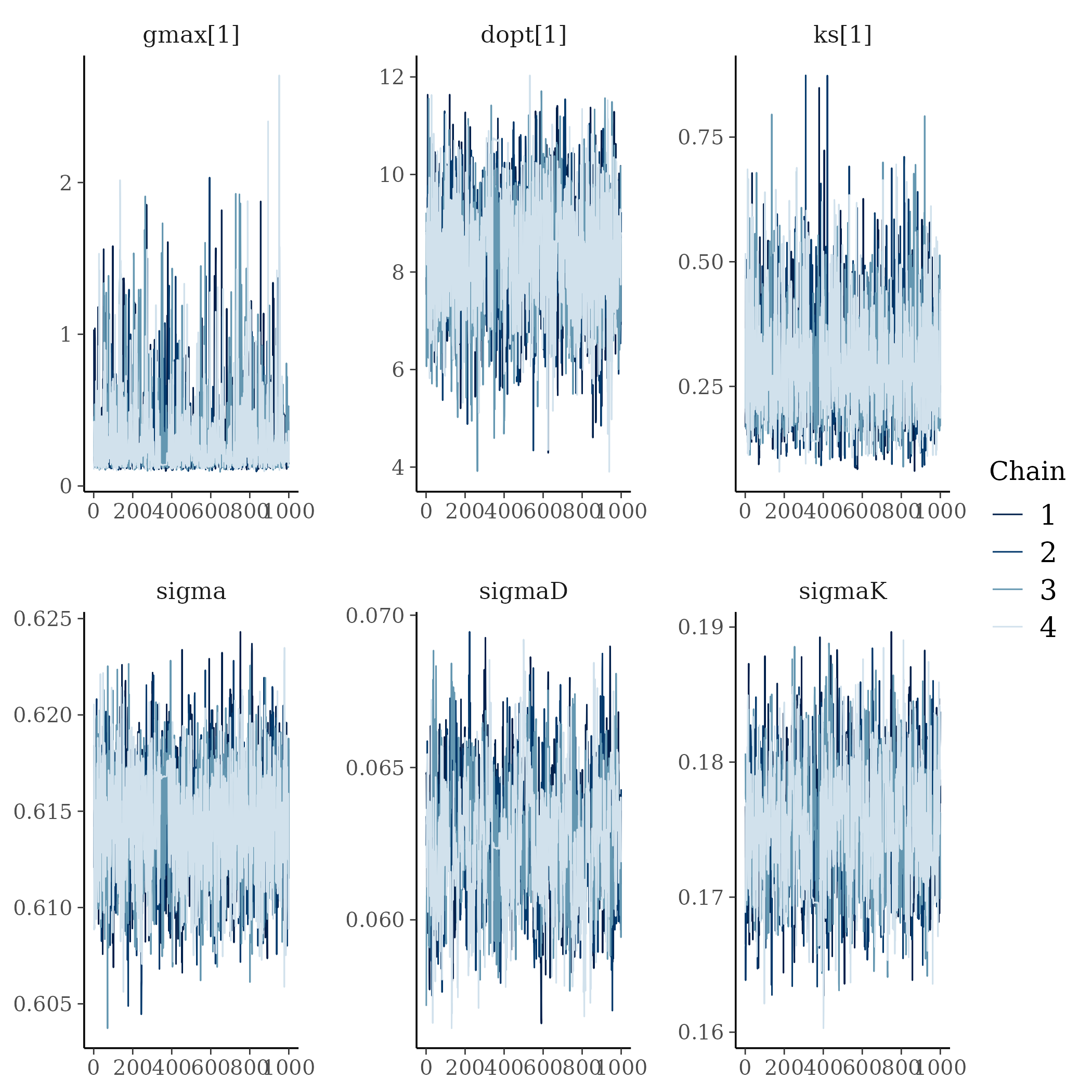
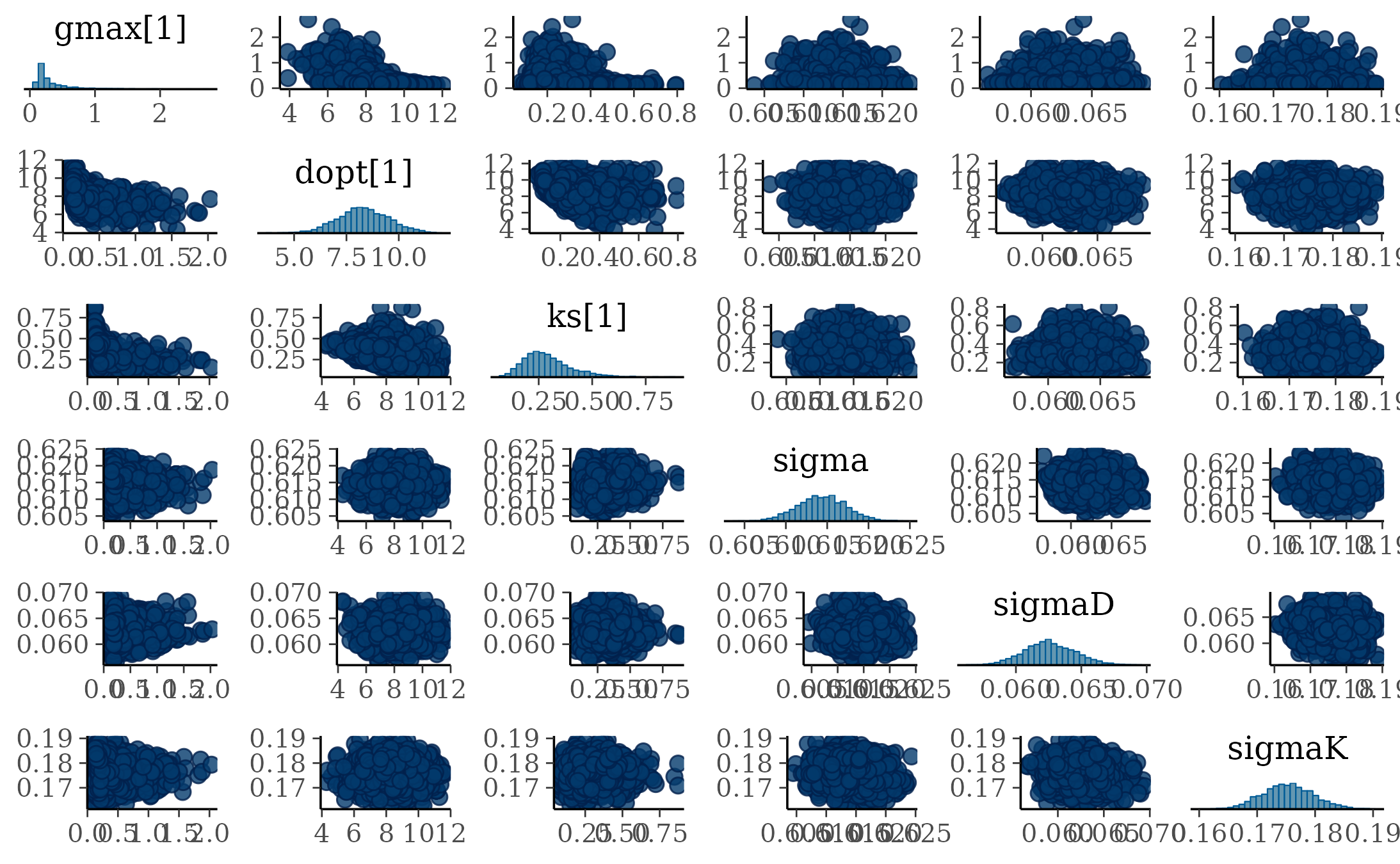
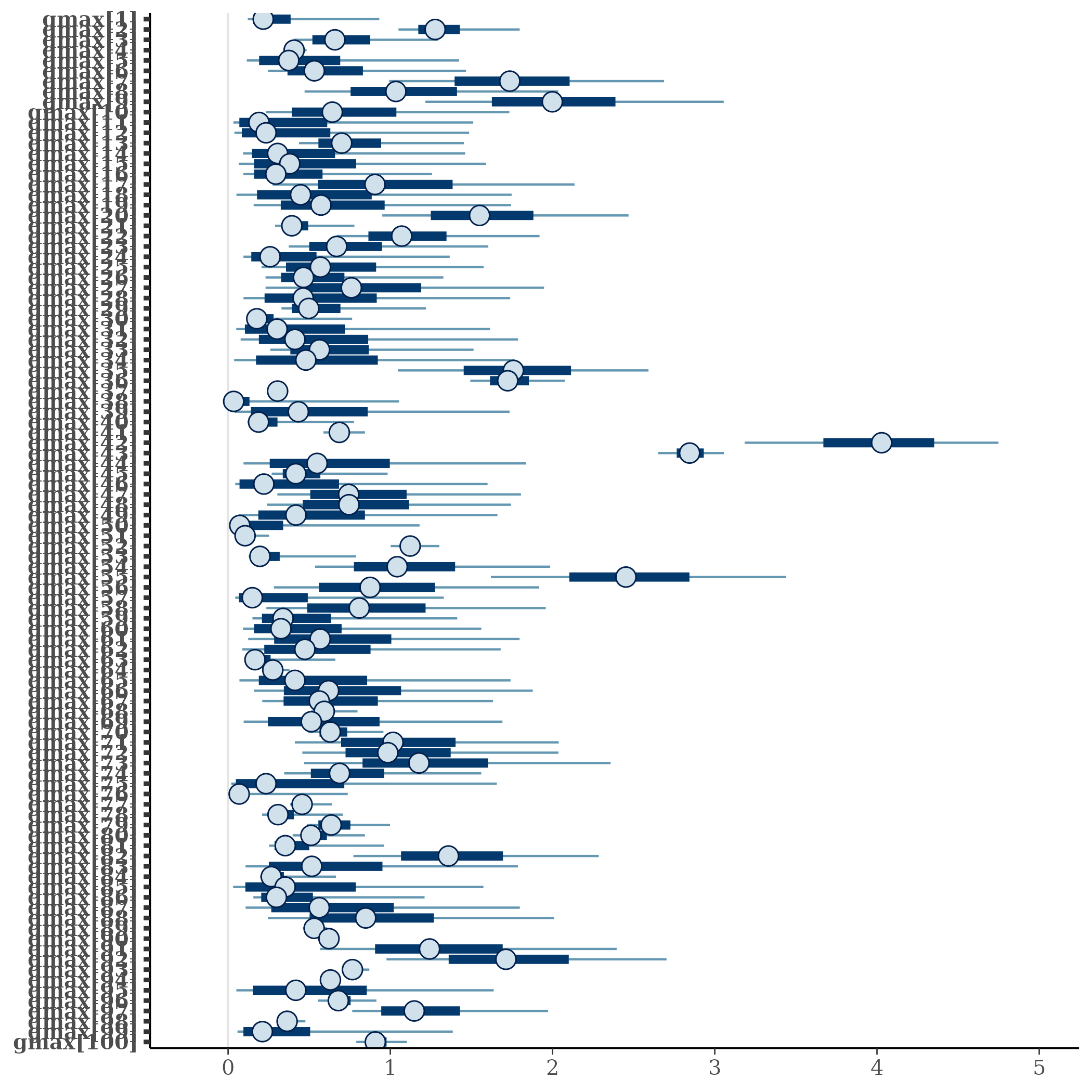
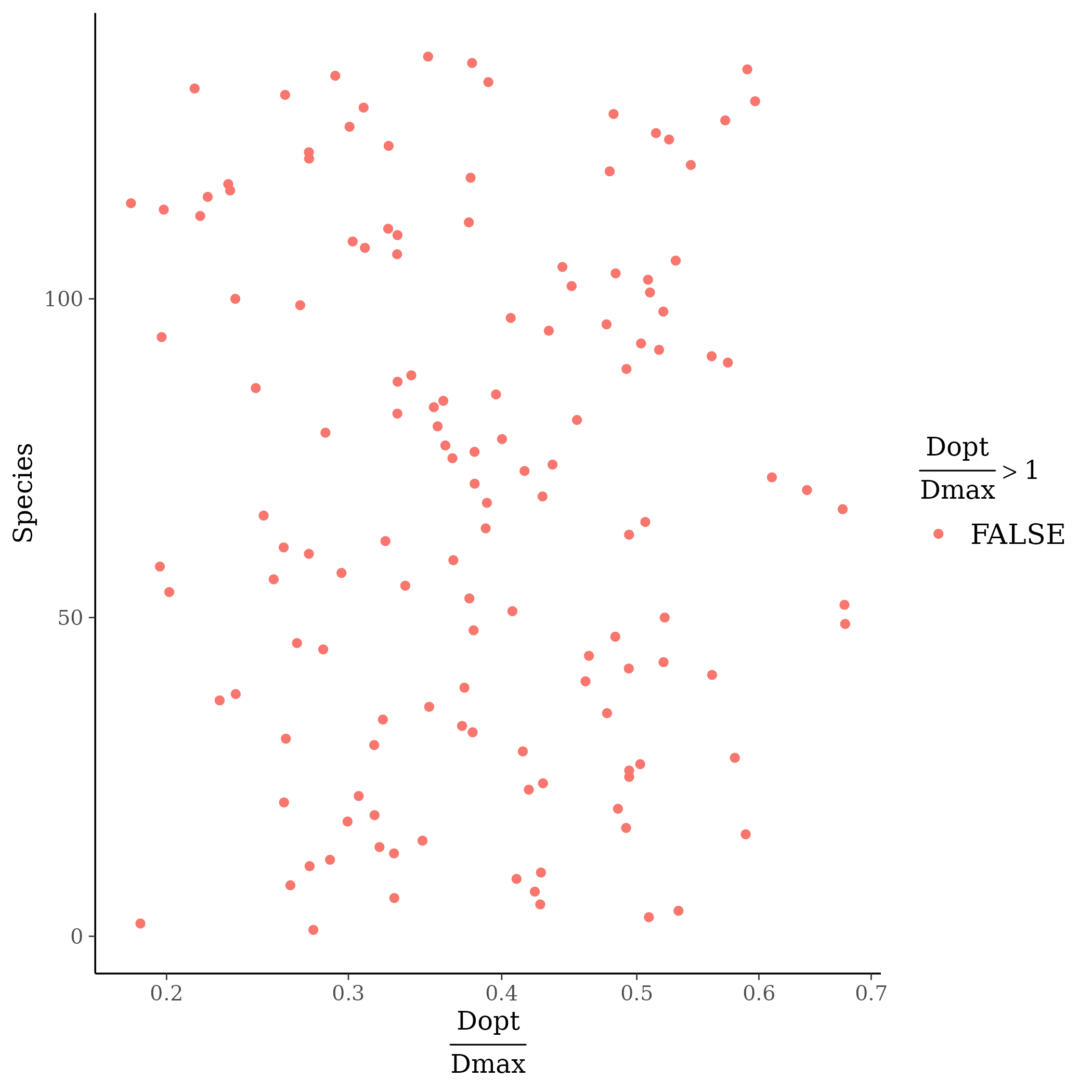
The model correctly converged (\(\hat R < 1.05\)) for all except one \(Gmax_i\) (still below \(\hat R < 1.1\)). The parameters doesn’t show correlations. \(Gmax_i\) posteriors have logical uncertainty but are varying widely among individuals and are not constrained by the superior limit. \(Dopt_s\) are all strictly below \(Dmax\).

References

Gompertz, B. (1825). On the nature of the function expressive of the law of humanmortality, and on a newmode of determining the value of life contingencies. Philosophical Transactions of the Royal Society of London, 115, 513–583. Retrieved from https://www.tandfonline.com/doi/full/10.1080/14786445908642737

Hérault, B., Bachelot, B., Poorter, L., Rossi, V., Bongers, F., Chave, J., Paine, C.E.T., Wagner, F. & Baraloto, C. (2011). Functional traits shape ontogenetic growth trajectories of rain forest tree species. Journal of Ecology, 99, 1431–1440.